Publications
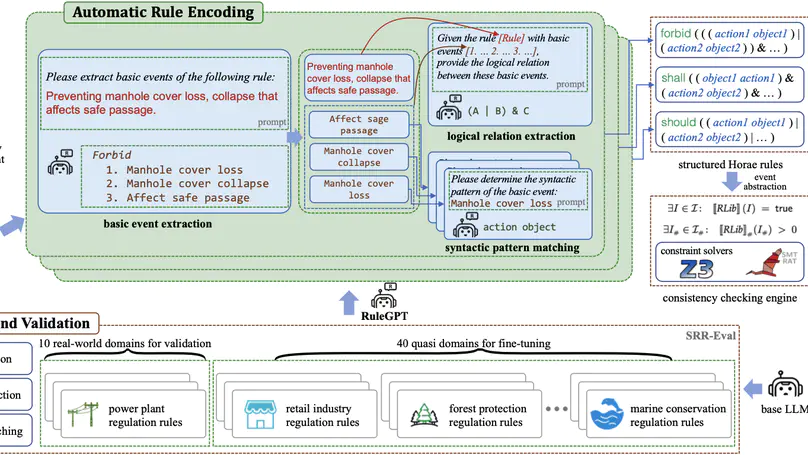
Artificial intelligence is rapidly encroaching on the field of service regulation. However, existing AI-based regulation techniques are often tailored to specific application domains and thus are difficult to generalize in an automated manner. This paper presents Horae, a unified specification language for modeling (multimodal) regulation rules across a diverse set of domains. We showcase how Horae facilitates an intelligent service regulation pipeline by further exploiting a fine-tuned large language model named RuleGPT that automates the Horae modeling process, thereby yielding an end-to-end framework for fully automated intelligent service regulation. The feasibility and effectiveness of our framework are demonstrated over a benchmark of various real-world regulation domains. In particular, we show that our open-sourced, fine-tuned RuleGPT with 7B parameters suffices to outperform GPT-3.5 and perform on par with GPT-4o.
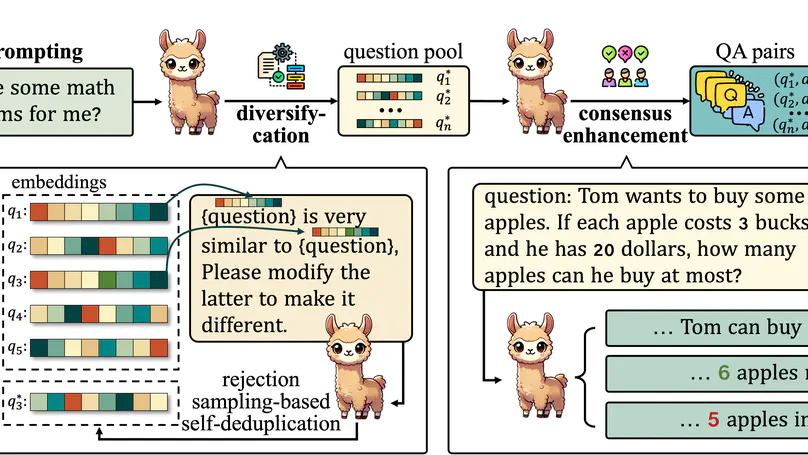
Self-improving large language models (LLMs) – i.e., to improve the performance of an LLM by fine-tuning it with synthetic data generated by itself – is a promising way to advance the capabilities of LLMs while avoiding extensive supervision. Existing approaches to self-improvement often rely on external supervision signals in the form of seed data and/or assistance from third-party models. This paper presents Crescent – a simple yet effective framework for generating high-quality synthetic question-answer data in a fully autonomous manner. Crescent first elicits the LLM to generate raw questions via a bait prompt, then diversifies these questions leveraging a rejection sampling-based self-deduplication, and finally feeds the questions to the LLM and collects the corresponding answers by means of majority voting. We show that Crescent sheds light on the potential of true self-improvement with zero external supervision signals for math reasoning; in particular, Crescent-generated question-answer pairs suffice to (i) improve the reasoning capabilities of an LLM while preserving its general performance (especially in the 0-shot setting); and (ii) distil LLM knowledge to weaker models more effectively than existing methods based on seed-dataset augmentation.
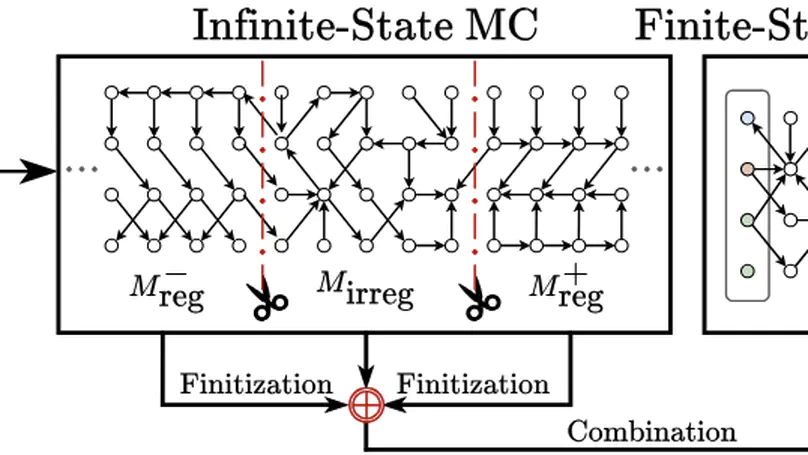
This paper introduces $k$-d PCPs – the class of probabilistic counter programs with $k \in \mathbb{N}$ counter variables inducing possibly infinite-state Markov chains. We show that the universal (positive) almost-sure termination problem is undecidable for $k$-d PCPs in general, yet decidable for $1$-d PCPs. We present an efficient decision procedure for the latter leveraging the technique of Markov chain finitization. Moreover, we identify several classes of $k$-d PCPs that are reducible to $1$-d PCPs – thus their termination properties can be inferred automatically. Experiments demonstrate that our decision procedure can certify (positive) almost-sure termination – without resorting to invariants or supermartingales – of non-trivial probabilistic programs beyond the scope of existing tools.

With continuous advances in physical technology, the number of qubits has increased from just a few to several thousand. To further extend the scale, the density of control lines has become one of the major limitations that decide the cost, heat dissipation, and fidelity. Specifically, each qubit requires dedicated control lines to manipulate its state, but these lines introduce additional thermal noise, degrading overall computational fidelity. Inspired from colinear signal transmission, a promising solution is to adopt multiplexing methods—such as frequency-division multiplexing (FDM) and time-division multiplexing (TDM)—to share control lines among qubits. However, existing methods lack a systematic architectural approach to support multiplexing-aware wiring, which leads to low parallelism and high crosstalk during deployment. In this work, we propose a multiplexing-aware design for the peripheral control lines of quantum processors, combining cryostat-level wiring optimization with on-chip routing. Our key novelty lies in a hybrid multiplexing architecture that adopts FDM for XY control and readout lines, and TDM for Z control lines. This enables high utilization of natural non-parallel operations, thereby cutting the additional circuit depth for TDM control. Finally, we develop an interaction model that co-optimizes qubit layout and multiplexed channel allocation. Our experiments are conducted on a self-developed quantum platform with 6x6 Xmon qubits. The results show that YOUTIAO achieves a 67.7% reduction in cryostat-level wiring complexity and overall superconducting quantum system costs, while reducing on-chip routing area by 23%. With these improvements, we still keep the 1q-gate fidelity at 99.98%, and only introduce 5% extra latency compared to the non-multiplexing system.
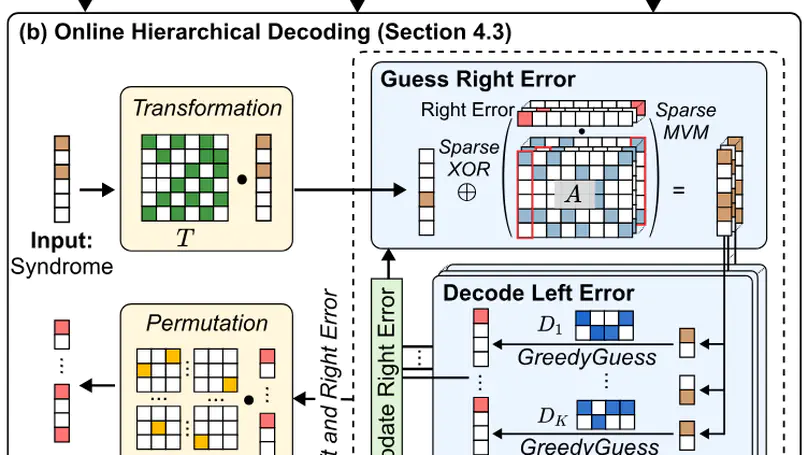
Quantum Low-Density Parity-Check (qLDPC) codes are a promising class of quantum error-correcting codes that exhibit constant-rate encoding and high error thresholds, thereby facilitating scalable fault-tolerant quantum computation. However, real-time decoding of qLDPC codes remains a significant challenge due to the high connectivity of their check matrices, which typically requires solving large-scale linear systems with sparse structures. In particular, off-the-shelf qLDPC decoders are often subject to a tradeoff between accuracy and latency, thus yielding no accurate and real-time decoding. This paper presents Vegapunk, a software-hardware co-design framework that enables real-time qLDPC decoding with high accuracy. To improve decoding accuracy, we design an offline decoupling strategy leveraging Satisfiability Modulo Theories (SMT) optimizations to mitigate quantum degeneracy; To enable fast decoding, we introduce an online hierarchical decoding algorithm employing a greedy strategy. Furthermore, we show that our SMT-optimized strategy suffices to produce decoupled matrices with maximized sparsity, thus admitting a dedicated accelerator to fully exploit the sparsity and parallelism to achieve real-time qLDPC decoding. Experimental results demonstrate that Vegapunk enables real-time decoding (< 1μs) for the Bivariate Bicycle (BB) code up to [[784,24,24]] while exhibiting logical error rates on par with the state-of-the-art decoder, e.g., BP+OSD.
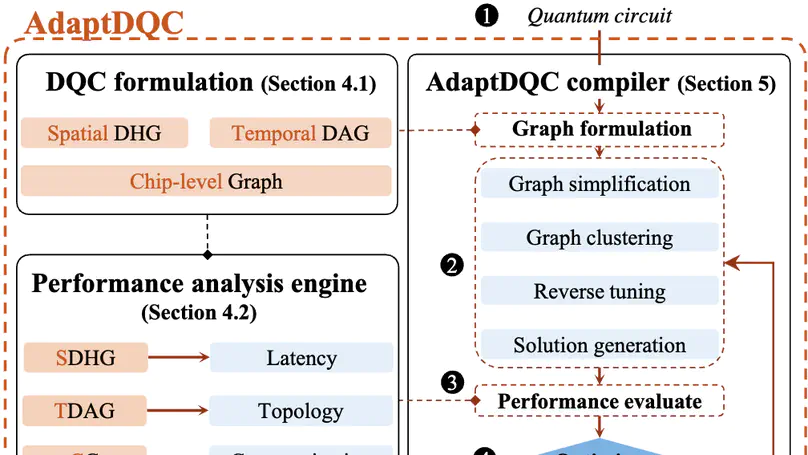
We present AdaptDQC, an adaptive compiler framework for optimizing distributed quantum computing (DQC) under diverse performance metrics and inter-chip communication (ICC) architectures. AdaptDQC leverages a novel spatial-temporal graph model to describe quantum circuits, model ICC architectures, and quantify critical performance metrics in DQC systems, yielding a systematic and adaptive approach to constructing circuit-partitioning and chip-mapping strategies that admit hybrid ICC architectures and are optimized against various objectives. Experimental results on a collection of benchmarks show that AdaptDQC outperforms state-of-the-art compiler frameworks: It reduces, on average, the communication cost by up to 40.2% and the latency by up to 38.4%.
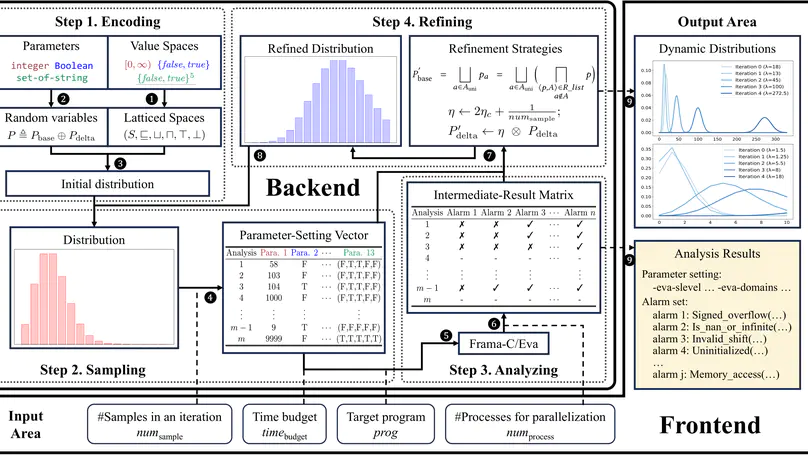
We launch Parf – a toolkit for adaptively tuning abstraction strategies of static program analyzers in a fully automated manner. Parf models various types of external parameters (encoding abstraction strategies) as random variables subject to probability distributions over latticed parameter spaces. It incrementally refines the probability distributions based on accumulated intermediate results generated by repeatedly sampling and analyzing, thereby ultimately yielding a set of highly accurate abstraction strategies. Parf is implemented on top of Frama-C/Eva – an off-the-shelf open-source static analyzer for c programs. Parf provides a web-based user interface facilitating the intuitive configuration of static analyzers and visualization of dynamic distribution refinement of the abstraction strategies. It further supports the identification of dominant parameters in Frama-C/Eva analysis. Benchmark experiments and a case study demonstrate the competitive performance of Parf for analyzing complex, large-scale real-world programs.
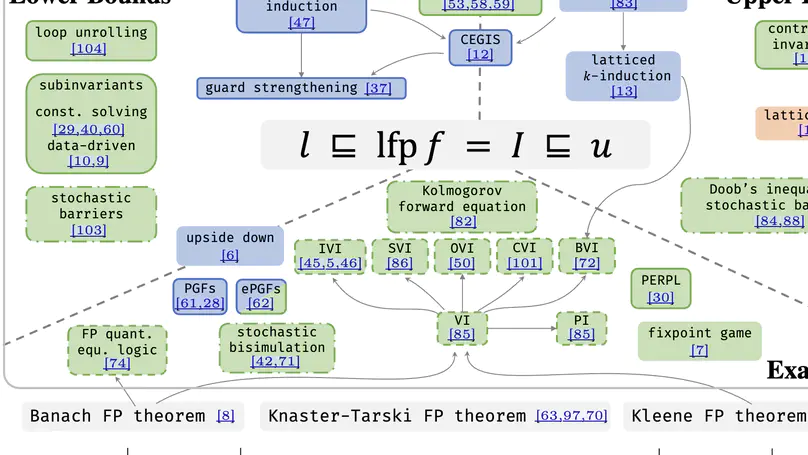
Fixed points are mathematical objects that are commonly employed in computer science to characterize key properties of iterative or cyclic behaviors, e.g., unbounded loops and recursions in programs or cycles in transition systems. Reasoning about such behaviors is arguably the hardest task in formal verification. The problem is even harder for stochastic systems as it often amounts to inferring quantitative fixed points that are highly intractable in practice. This article surveys recent advancements in fixed-point reasoning for stochastic systems modeled as probabilistic programs, probabilistic transition systems, and stochastic hybrid systems and outlines potential directions for future research thereof. The core of our results is the fixed-point reasoning landscape for stochastic systems, where we focus on formal techniques that either (i) establish sound over-/under-approximations of quantitative fixed points; or (ii) infer the exact fixed points for a restricted class of systems.
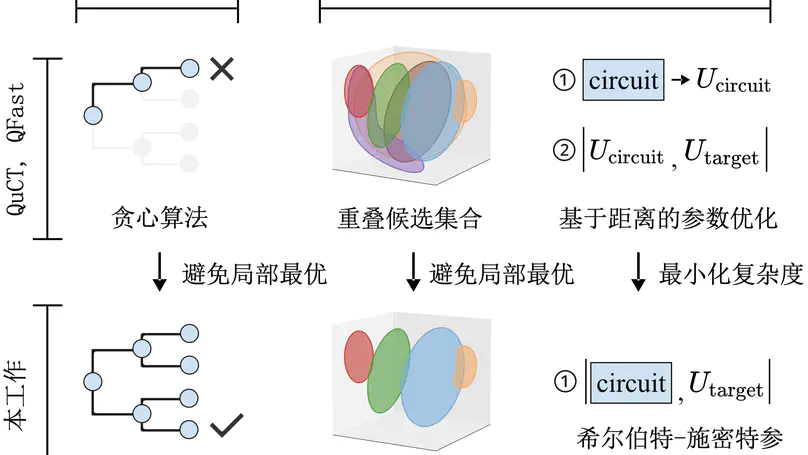
Current quantum programs are usually represented as quantum circuits, including various quantum gates. If the program contains gates that are represented as unitary matrices, these gates need to be transformed into quantum circuits composed of basic gates. However, current synthesis methods may generate inferior circuits with thousands of gates, which leads to failure when deploying to real-world quantum hardware. Moreover, the process to minimize the number of gate takes weeks or even months when the number of qubits goes to 8. In this work, we propose Fast-USYN that enables fast synthesis from unitary to high-quality quantum circuits. We first introduce an iterative approach that approximates the target unitary by inserting circuit blocks. The minimization of gates is achieved by a look-ahead strategy with a rewarding mechanism to reduce redundant gates. In the acceleration of unitary synthesis, instead of exhaustively enumerating tremendous candidates, we construct the search space by depicting the closure of each candidate. Furthermore, to reduce the overhead of searching the optimal gate parameters, we pack the selected candidates with the target unitary into a uniform circuit so that we can quickly obtain the approximation distance by calculating its expectation on the ground state. Experiments show that Fast-USYN achieves 1.6-2.7 times gate reduction and 3.7-20.6 times speedup for 5-qubit to 8-qubit synthesis, compared to QuCT and QFAST.

Verifying probabilistic programs requires reasoning about various probabilistic behaviors, e.g., random sampling, nondeterminism, and conditioning, against multiple quantitative properties, e.g., assertion-violation probabilities, moments, and expected running times. It is desirable and theoretically significant to have a unified framework which can deal with quantitative analysis of programs with different probabilistic behaviors and properties. In this paper, we present a unified framework for the quantitative analysis of probabilistic programs, which incorporates and extends existing results on the analysis of termination, temporal properties, and expected cost. We show that these quantitative properties of a general probabilistic program can be characterized as solutions to equation systems of the corresponding Markov chain counterpart with a possibly uncountable state space. Based on such characterization, we propose sufficient conditions to establish upper and lower bounds on these quantitative properties. Moreover, we demonstrate how our approach can be adapted to address inference problems in Bayesian programming.
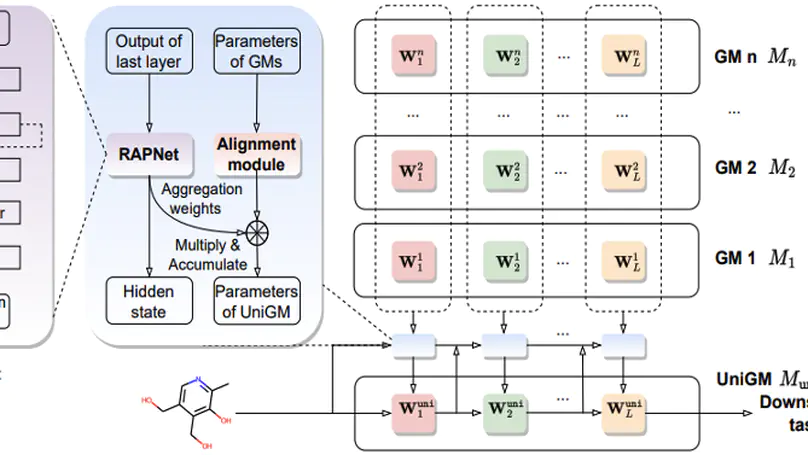
Recent years have witnessed remarkable advances in graph representation learning using Graph Neural Networks (GNNs). To fully exploit the unlabeled graphs, researchers pre-train GNNs on large-scale graph databases and then fine-tune these pre-trained Graph Models (GMs) for better performance in downstream tasks. Because different GMs are developed with diverse pre-training tasks or datasets, they can be complementary to each other for a more complete knowledge base. Naturally, a compelling question is emerging: How can we exploit the diverse knowledge captured by different GMs simultaneously in downstream tasks? In this paper, we make one of the first attempts to exploit multiple GMs to advance the performance in the downstream tasks. More specifically, for homogeneous GMs that share the same model architecture but are obtained with different pre-training tasks or datasets, we align each layer of these GMs and then aggregate them adaptively on a per-sample basis with a tailored Recurrent Aggregation Policy Network (RAPNet). For heterogeneous GMs with different model architectures, we design an alignment module to align the output of diverse GMs and a meta-learner to decide the importance of each GM conditioned on each sample automatically before aggregating the GMs. Extensive experiments on various downstream tasks from 3 domains reveal our dominance over each single GM. Additionally, our methods (UniGM) can achieve better performance with moderate computational overhead compared to alternative approaches including ensemble and model fusion. Also, we verify that our methods are not limited to graph data but could be flexibly applied to image and text data. The code can be seen in the anonymous link: https://anonymous.4open.science/r/UniGM-DA65.
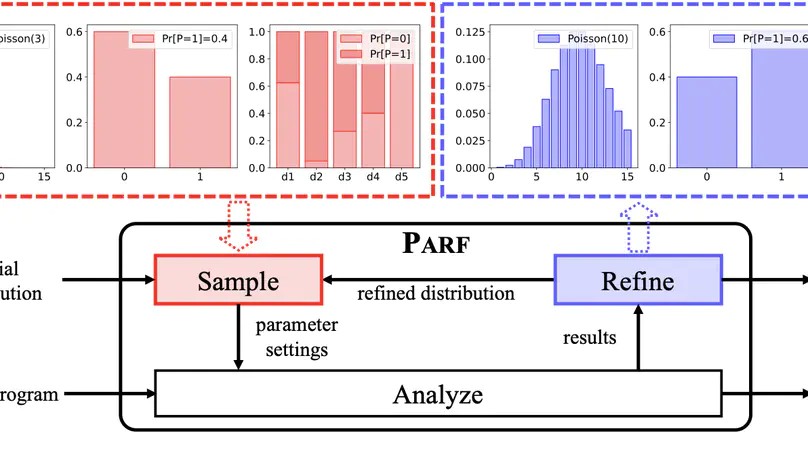
Abstract interpretation is a key formal method for the static analysis of programs. The core challenge in applying abstract interpretation lies in the configuration of abstraction and analysis strategies encoded by a large number of external parameters of static analysis tools. To attain low false-positive rates (i.e., accuracy) while preserving analysis efficiency, tuning the parameters heavily relies on expert knowledge and is thus difficult to automate. In this paper, we present a fully automated framework called Parf to adaptively tune the external parameters of abstract interpretation-based static analyzers. Parf models various types of parameters as random variables subject to probability distributions over latticed parameter spaces. It incrementally refines the probability distributions based on accumulated intermediate results generated by repeatedly sampling and analyzing, thereby ultimately yielding a set of highly accurate parameter settings within a given time budget. We have implemented Parf on top of Frama-C/Eva – an off-the-shelf open-source abstract interpretation-based static analyzer for C programs – and compared it against the expert refinement strategy and Frama-C/Eva’s official configurations over the Frama-C OSCS benchmark. Experimental results indicate that Parf achieves the lowest number of false positives on 34/37 (91.9%) program repositories with exclusively best results on 13/37 (35.1%) cases. In particular, Parf exhibits promising performance for analyzing complex, large-scale real-world programs.

Proving equivalence between functional programs is a fundamental problem in program verification, which often amounts to reasoning about algebraic data types (ADTs) and compositions of structural recursions. Modern theorem provers provide structural induction for such reasoning, but a structural induction on the original theorem is often insufficient for many equivalence theorems. In such cases, one has to invent a set of lemmas, prove these lemmas by additional induction, and use these lemmas to prove the original theorem. There is, however, a lack of systematic understanding of what lemmas are needed for inductive proofs and how these lemmas can be synthesized automatically. This paper presents directed lemma synthesis, an effective approach to automating equivalence proofs by discovering critical lemmas using program synthesis techniques. We first identify two induction-friendly forms of propositions that give formal guarantees to the progress of the proof. We then propose two tactics that synthesize and apply lemmas, thereby transforming the proof goal into induction-friendly forms. Both tactics reduce lemma synthesis to a set of independent and typically small program synthesis problems that can be efficiently solved. Experimental results demonstrate the effectiveness of our approach: Compared to state-of-the-art equivalence checkers employing heuristic-based lemma enumeration, directed lemma synthesis saves 95.47% runtime on average and solves 38 more tasks over an extended version of the standard benchmark set.
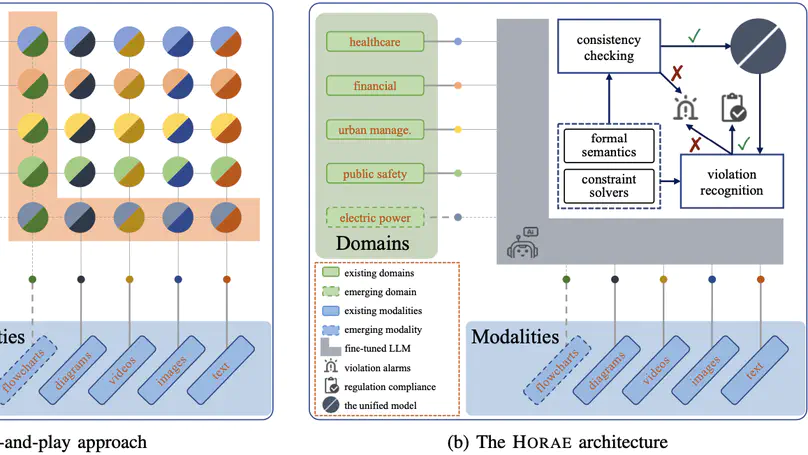
Artificial intelligence is rapidly encroaching on the field of service regulation. This work-in-progress article presents the design principles behind Horae, a unified specification language to model multimodal regulation rules across a diverse set of domains. We show how Horae facilitates an intelligent service regulation pipeline by further exploiting a fine-tuned large language model named RuleGPT that automates the Horae modeling process, thereby yielding an end-to-end framework for fully automated intelligent service regulation.
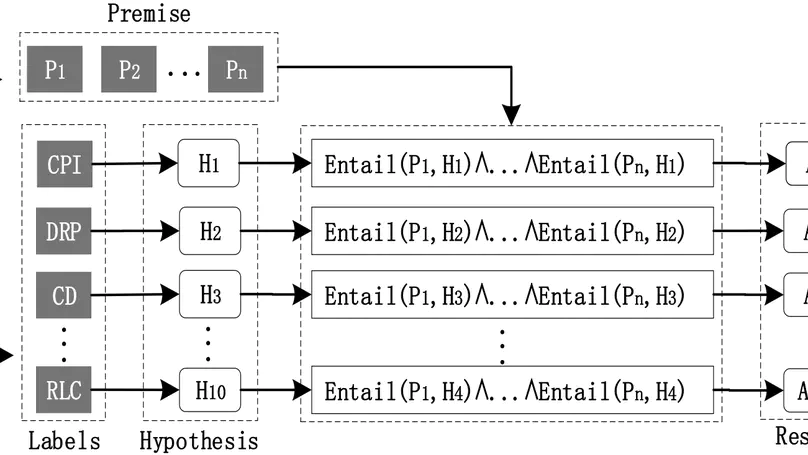
The advancement of AI-generated content (AIGC) drives the diversification of healthcare services, resulting in increased private information collection by healthcare service providers. Therefore, compliance with privacy regulations has increasingly become a paramount concern for both regulatory authorities and consumers. Privacy policies are crucial for consumers to understand how their personal information is collected, stored, and processed. In this work, we propose a privacy policy text compliance reasoning framework called FACTOR, which harnesses the power of large language models (LLMs). Since the General Data Protection Regulation (GDPR) has broad applicability, this work selects GDPR Article 13 as regulation requirements. FACTOR segments the privacy policy text using a sliding window strategy and employs LLM-based text entailment to assess compliance for each segment. The framework then applies a rule-based ensemble approach to aggregate the entailment results for all regulation requirements from GDPR. Our experiments on a synthetic corpus of 388 privacy policies demonstrate the effectiveness of FACTOR. Additionally, we analyze 100 randomly selected websites offering healthcare services, revealing that 9 of them lack a privacy policy altogether, while 29 have privacy policy texts that fail to meet the regulation requirements.
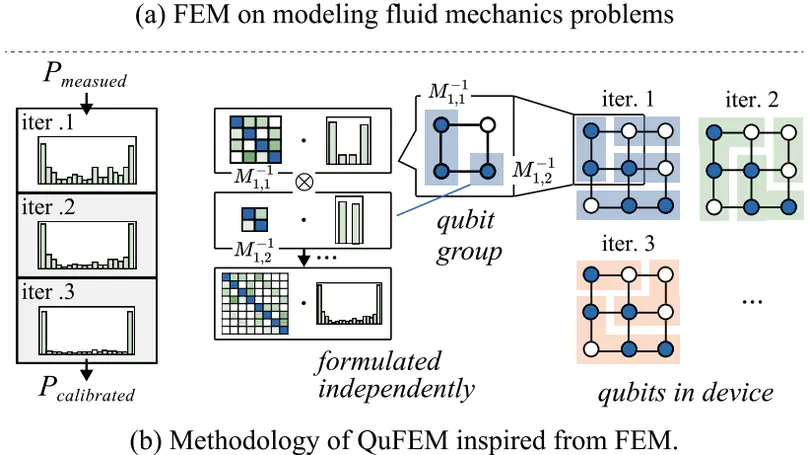
Quantum readout noise turns out to be the most significant source of error, which greatly affects the measurement fidelity. Matrix-based calibration has been demonstrated to be effective in various quantum platforms. However, existing methodologies are fundamentally limited in either scalability or accuracy. Inspired by the classical finite element method (FEM), a formal method to model the complex interaction between elements, we present our calibration framework named QuFEM. First, we apply a divide-and-conquer strategy that formulates the calibration as a series of tensor products with noise matrices. This matrices are iteratively characterized together with the calibrated probability distribution, aiming to capture the inherent locality of qubit interactions. Then, to accelerate the end-to-end calibration, we propose a sparse tensor-product engine to exploit the sparsity in the intermediate values. Our experiments show that QuFEM achieves $2.5 \times 10^{3}\times$ speedup in the 136-qubit calibration compared to the state-of-the-art matrix-based calibration technique, and provides 1.2$\times$ and 1.4$\times$ fidelity improvement on the 18-qubit and 36-qubit real-world quantum devices.
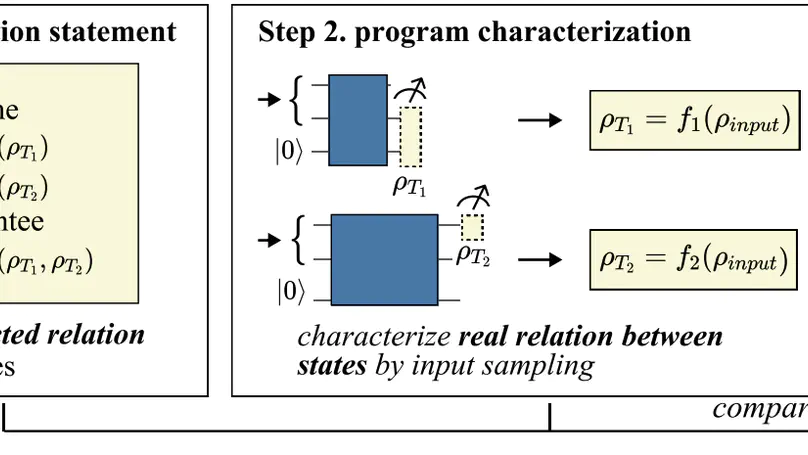
Unlike classical computing, quantum program verification (QPV) is much more challenging due to the non-duplicability of quantum states that collapse after measurement. Prior approaches rely on deductive verification that shows poor scalability. Or they require exhaustive assertions that cannot ensure the program is correct for all inputs. In this paper, we propose MorphQPV, a confident assertion-based verification methodology. Our key insight is to leverage the isomorphism in quantum programs, which implies a structure-preserve relation between the program runtime states. In the assertion statement, we define a tracepoint pragma to label the verified quantum state and an assume-guarantee primitive to specify the expected relation between states. Then, we characterize the ground-truth relation between states using an isomorphism-based approximation, which can effectively obtain the program states under various inputs while avoiding repeated executions. Finally, the verification is formulated as a constraint optimization problem with a confidence estimation model to enable rigorous analysis. Experiments suggest that MorphQPV reduces the number of program executions by $107.9\times$ when verifying the 27-qubit quantum lock algorithm and improves the probability of success by $3.3\times$-$9.9\times$ when debugging five benchmarks.

During software development, vulnerabilities have posed a significant threat to users. Applying patches is the most effective way to combat vulnerabilities. In a large scale software system, testing the presence of a security patch in every affected binary is crucial to ensure system security. Identifying whether a binary has been patched for a known vulnerability is challenging, as there may only be small differences between patched and vulnerable versions. Existing approaches mainly focus on detecting patches that are compiled in the same compiler options. However, it is common for developers to compile programs with very different compiler options in different situations, which causes inaccuracy for existing methods. In this paper, we propose a new approach named PS3, referring to precise patch presence test based on semantic-level symbolic signature. PS3 exploits symbolic emulation to extract signatures that are stable under different compiler options. Then, PS3 can test the presence of the patch precisely by comparing the signatures between the reference and the target at a semantic level. To evaluate the effectiveness of our approach, we constructed a dataset consisting of 3,631 (CVE, binary) pairs of 62 recent CVEs in four C/C++ projects. The experimental results show that PS3 achieves scores of 0.82, 0.97, and 0.89 in terms of precision, recall, and F1 score, respectively. PS3 outperforms the state-of-the-art baselines by improving 33% in terms of F1 score and remains stable in different compiler options.
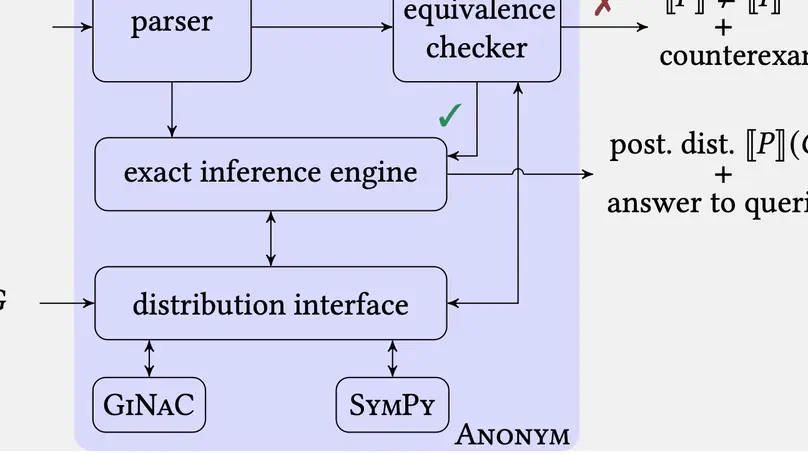
We present an exact Bayesian inference method for inferring posterior distributions encoded by probabilistic programs featuring possibly unbounded loops. Our method is built on a denotational semantics represented by probability generating functions, which resolves semantic intricacies induced by intertwining discrete probabilistic loops with conditioning (for encoding posterior observations). We implement our method in a tool called Prodigy; it augments existing computer algebra systems with the theory of generating functions for the (semi-)automatic inference and quantitative verification of conditioned probabilistic programs. Experimental results show that Prodigy can handle various infinite-state loopy programs and exhibits comparable performance to state-of-the-art exact inference tools over loop-free benchmarks.
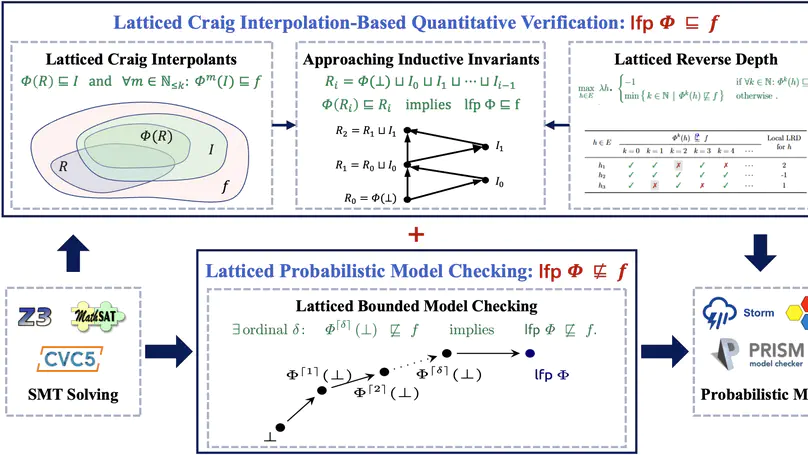
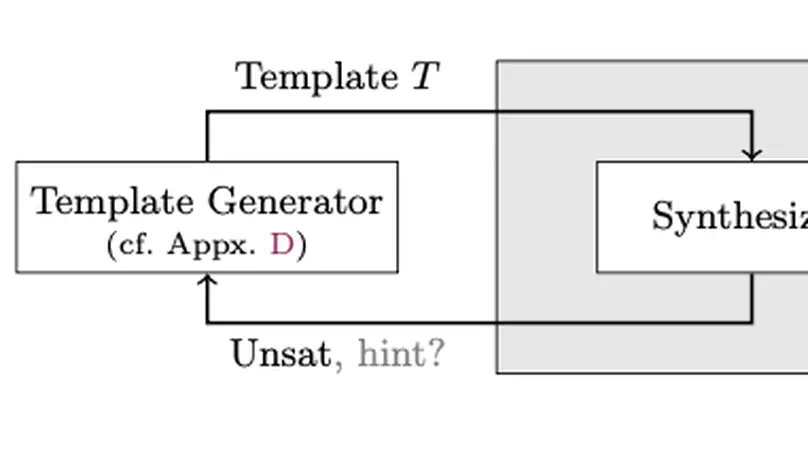
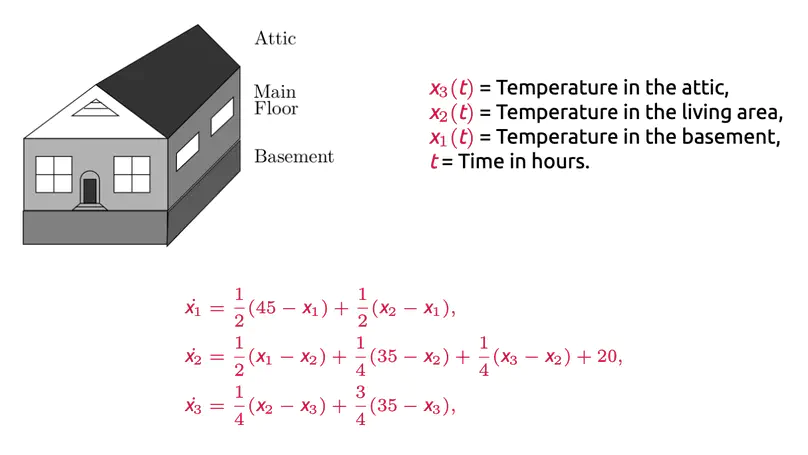
In this work, we are primarily concerned with the question: Is Craig interpolation applicable to the automatic, quantitative verification of (infinite-state) probabilistic programs with potentially unbounded loops? Our preliminary results indicate an affirmative answer:
- Quantitative Craig interpolants. We propose a quantitative version of Craig interpolants by extending predicates to expectations (expected values), which can be used to discover quantitative loop invariants that suffice to establish upper bounds on the least fixed point;
- Latticed Craig interpolation. We present latticed Craig interpolation by exploiting quantitative interpolants over complete lattices, which conservatively extends both McMillan’s interpolation-based SAT model checking (to the quantitative setting) and Batz et al.’s latticed bounded model checking (to the unbounded case);
- Soundness and Completeness. We show that our latticed interpolation procedure is sound and establish sufficient conditions under which it is further complete.
- Synthesizing quantitative interpolants. We (semi-)automated our verification procedure by employing a counterexample-guided inductive synthesis framework to automatically generate quantitative interpolants. Our implementation shows promise: It finds invariants for non-trivial infinite-state programs with unbounded loops.
Essential tasks for the verification of probabilistic programs include bounding expected outcomes and proving termination in finite expected runtime. We contribute a simple yet effective inductive synthesis approach for proving such quantitative reachability properties by generating inductive invariants on source-code level. Our implementation shows promise: It finds invariants for (in)finite-state programs, can beat state-of-the-art probabilistic model checkers, and is competitive with modern tools dedicated to invariant synthesis and expected runtime reasoning.
We present a new proof rule for verifying lower bounds on quantities of probabilistic programs. Our proof rule is not confined to almost-surely terminating programs – as is the case for existing rules – and can be used to establish non-trivial lower bounds on, e.g., termination probabilities and expected values, for possibly divergent probabilistic loops, e.g., the well-known three-dimensional random walk on a lattice.
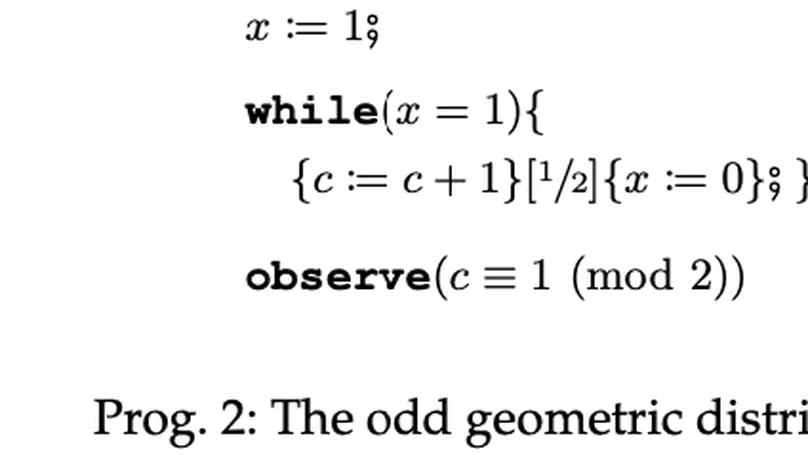
Probabilistic programs are typically normal-looking programs describing posterior probability distributions. They intrinsically code up randomized algorithms and have long been at the heart of modern machine learning and approximate computing. We explore the theory of generating functions and investigate its usage in the exact quantitative reasoning of probabilistic programs. Important topics include the exact representation of program semantics, proving exact program equivalence, and – as our main focus in this extended abstract – exact probabilistic inference. In probabilistic programming, inference aims to derive a program’s posterior distribution. In contrast to approximate inference, inferring exact distributions comes with several benefits, e.g., no loss of precision, natural support for symbolic parameters, and efficiency on models with certain structures. Exact probabilistic inference, however, is a notoriously hard task. The challenges mainly arise from three program constructs: (1) unbounded while-loops and/or recursion, (2) infinite-support distributions, and (3) conditioning (via posterior observations). We present our ongoing research in addressing these challenges (with a focus on conditioning) leveraging generating functions and show their potential in facilitating exact probabilistic inference for discrete probabilistic programs.

We present the invariant barrier-certificate condition that witnesses unbounded-time safety of differential dynamical systems. The proposed condition is the weakest possible one to attain inductive invariance. We show that discharging the invariant barrier-certificate condition —thereby synthesizing invariant barrier certificates— can be encoded as solving an optimization problem subject to bilinear matrix inequalities (BMIs). We further propose a synthesis algorithm based on difference-of-convex programming, which approaches a local optimum of the BMI problem via solving a series of convex optimization problems. This algorithm is incorporated in a branch-and-bound framework that searches for the global optimum in a divide-and-conquer fashion. We present a weak completeness result of our method, namely, a barrier certificate is guaranteed to be found (under some mild assumptions) whenever there exists an inductive invariant (in the form of a given template) that suffices to certify safety. Experimental results on benchmarks demonstrate the effectiveness and efficiency of our approach.
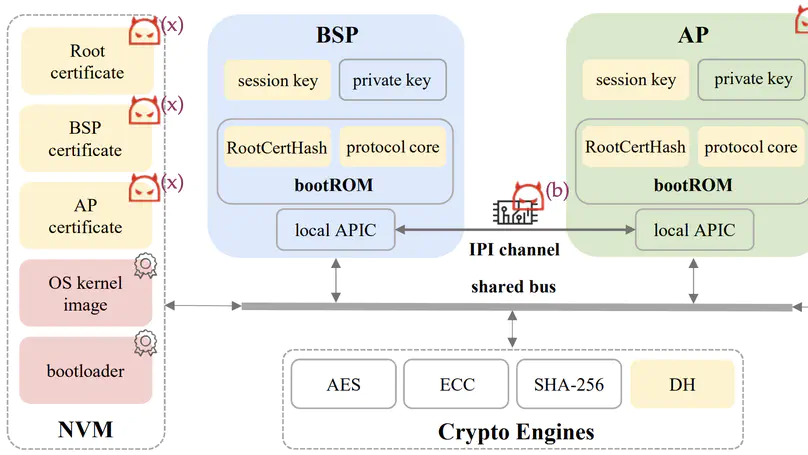
Hardware supply-chain attacks are raising significant security threats to the boot process of multiprocessor systems. This paper identifies a new, prevalent hardware supply-chain attack surface that can bypass multiprocessor secure boot due to the absence of processor-authentication mechanisms. To defend against such attacks, we present PA-Boot, the first formally verified processor-authentication protocol for secure boot in multiprocessor systems. PA-Boot is proved functionally correct and is guaranteed to detect multiple adversarial behaviors, e.g., processor replacements, man-in-the-middle attacks, and tampering with certificates. The fine-grained formalization of PA-Boot and its fully mechanized security proofs are carried out in the Isabelle/HOL theorem prover with 306 lemmas/theorems and ~7,100 LoC. Experiments on a proof-of-concept implementation indicate that PA-Boot can effectively identify boot-process attacks with a considerably minor overhead and thereby improve the security of multiprocessor systems.

We study discrete probabilistic programs with potentially unbounded looping behaviors over an infinite state space. We present, to the best of our knowledge, the first decidability result for the problem of determining whether such a program generates exactly a specified distribution over its outputs (provided the program terminates almost-surely). The class of distributions that can be specified in our formalism consists of standard distributions (geometric, uniform, etc.) and finite convolutions thereof. Our method relies on representing these (possibly infinite-support) distributions as probability generating functions which admit effective arithmetic operations. We have automated our techniques in a tool called Prodigy, which supports automatic invariance checking, compositional reasoning of nested loops, and efficient queries to the output distribution, as demonstrated by experiments.
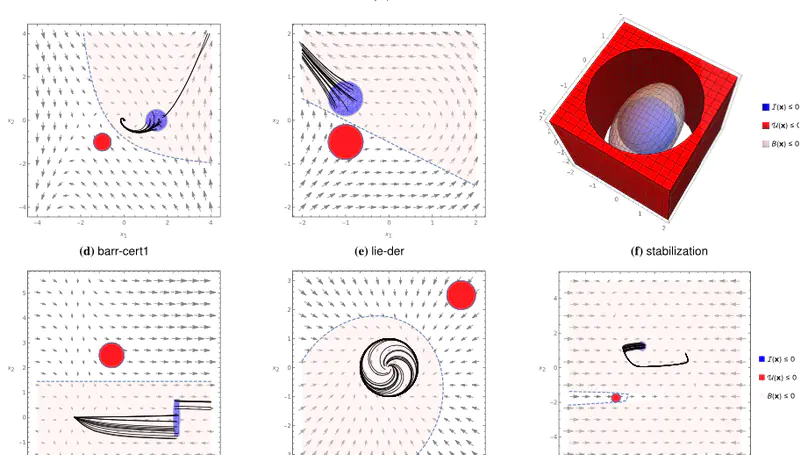
A barrier certificate often serves as an inductive invariant that isolates an unsafe region from the reachable set of states, and hence is widely used in proving safety of hybrid systems possibly over the infinite time horizon. We present a novel condition on barrier certificates, termed the invariant barrier-certificate condition, that witnesses unbounded-time safety of differential dynamical systems. The proposed condition is by far the least conservative one on barrier certificates, and can be shown as the weakest possible one to attain inductive invariance. We show that discharging the invariant barrier-certificate condition—thereby synthesizing invariant barrier certificates—can be encoded as solving an optimization problem subject to bilinear matrix inequalities (BMIs). We further propose a synthesis algorithm based on difference-of-convex programming, which approaches a local optimum of the BMI problem via solving a series of convex optimization problems. This algorithm is incorporated in a branch-and-bound framework that searches for the global optimum in a divide-and-conquer fashion. We present a weak completeness result of our method, in the sense that a barrier certificate is guaranteed to be found (under some mild assumptions) whenever there exists an inductive invariant (in the form of a given template) that suffices to certify safety of the system. Experimental results on benchmark examples demonstrate the effectiveness and efficiency of our approach.
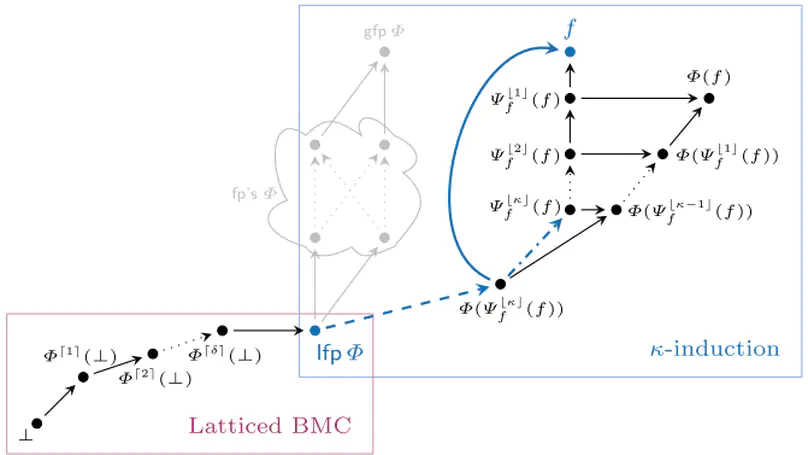
We revisit two well-established verification techniques, $k$-induction and bounded model checking (BMC), in the more general setting of fixed point theory over complete lattices. Our main theoretical contribution is latticed $k$-induction, which (i) generalizes classical $k$-induction for verifying transition systems, (ii) generalizes Park induction for bounding fixed points of monotonic maps on complete lattices, and (iii) extends from naturals $k$ to transfinite ordinals $\kappa$, thus yielding $\kappa$-induction. The lattice-theoretic understanding of $k$-induction and BMC enables us to apply both techniques to the fully automatic verification of infinite-state probabilistic programs. Our prototypical implementation manages to automatically verify non-trivial specifications for probabilistic programs taken from the literature that – using existing techniques – cannot be verified without synthesizing a stronger inductive invariant first.

We investigate the termination problem of a family of multi-path polynomial programs (MPPs), in which all assignments to program variables are polynomials, and test conditions of loops and conditional statements are polynomial equalities. We show that the set of non-terminating inputs (NTI) of such a program is algorithmically computable, thus leading to the decidability of its termination. To the best of our knowledge, the considered family of MPPs is hitherto the largest one for which termination is decidable. We present an explicit recursive function which is essentially Ackermannian, to compute the maximal length of ascending chains of polynomial ideals under a control function, and thereby obtain a complete answer to the questions raised by Seidenberg. This maximal length facilitates a precise complexity analysis of our algorithms for computing the NTI and deciding termination of MPPs. We extend our method to programs with polynomial guarded commands and show how an incomplete procedure for MPPs with inequality guards can be obtained. An application of our techniques to invariant generation of polynomial programs is further presented.

In this paper, we propose a method for bounding the probability that a stochastic differential equation (SDE) system violates a safety specification over the infinite time horizon. SDEs are mathematical models of stochastic processes that capture how states evolve continuously in time. They are widely used in numerous applications such as engineered systems (e.g., modeling how pedestrians move in an intersection), computational finance (e.g., modeling stock option prices), and ecological processes (e.g., population change over time). Previously the safety verification problem has been tackled over finite and infinite time horizons using a diverse set of approaches. The approach in this paper attempts to connect the two views by first identifying a finite time bound, beyond which the probability of a safety violation can be bounded by a negligibly small number. This is achieved by discovering an exponential barrier certificate that proves exponentially converging bounds on the probability of safety violations over time. Once the finite time interval is found, a finite-time verification approach is used to bound the probability of violation over this interval. We demonstrate our approach over a collection of interesting examples from the literature, wherein our approach can be used to find tight bounds on the violation probability of safety properties over the infinite time horizon.
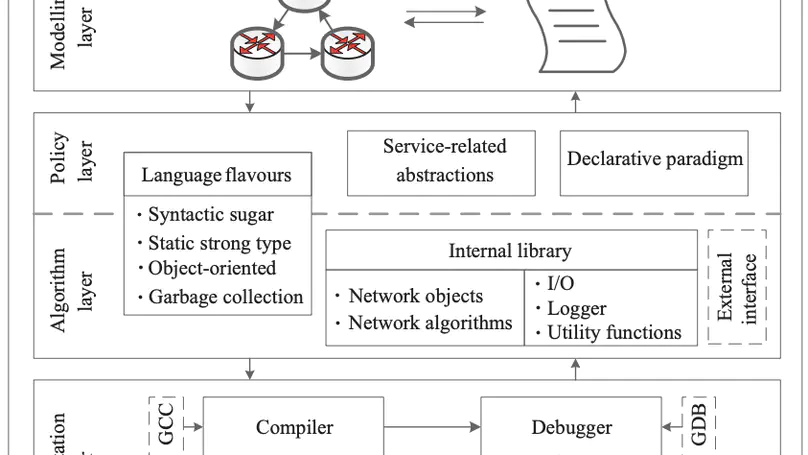
Software-defined networking (SDN) is a revolutionary technology that facilitates network management and enables programmatically efficient network configuration, thereby improving network performance and flexibility. However, as the application programming interfaces (APIs) of SDN are low-level or functionality-restricted, SDN programmers cannot easily keep pace with the ever-changing devices, topologies, and demands of SDN. By deriving motivation from industry practice, we define a novel network algorithm programming language (NAPL) that enhances the SDN framework with a rapid programming flow from topology-based network models to C++ implementations, thus bridging the gap between the limited capability of existing SDN APIs and the reality of practical network management. In contrast to several state-of-the-art languages, NAPL provides a range of critical high-level network programming features: (1) topology-based network modeling and visualization; (2) fast abstraction and expansion of network devices and constraints; (3) a declarative paradigm for the fast design of forwarding policies; (4) a built-in library for complex algorithm implementation; (5) full compatibility with C++ programming; and (6) user-friendly debugging support when compiling NAPL into highly readable C++ codes. The expressiveness and performance of NAPL are demonstrated in various industrial scenarios originating from practical network management.
We present an algorithm for active learning of deterministic timed automata with a single clock. The algorithm is within the framework of Angluin’s $L^*$ algorithm and inspired by existing work on the active learning of symbolic automata. Due to the need of guessing for each transition whether it resets the clock, the algorithm is of exponential complexity in the size of the learned automata. Before presenting this algorithm, we propose a simpler version where the teacher is assumed to be smart in the sense of being able to provide the reset information. We show that this simpler setting yields a polynomial complexity of the learning process. Both of the algorithms are implemented and evaluated on a collection of randomly generated examples. We furthermore demonstrate the simpler algorithm on the functional specification of the TCP protocol.
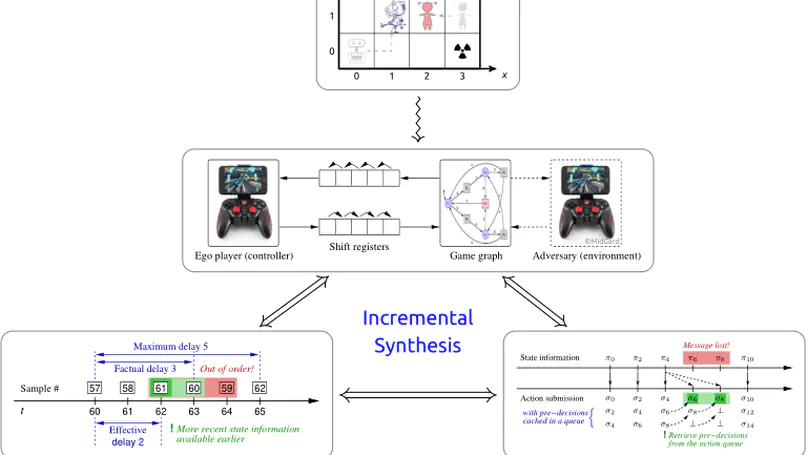
The possible interactions between a controller and its environment can naturally be modelled as the arena of a two-player game, and adding an appropriate winning condition permits to specify desirable behavior. The classical model here is the positional game, where both players can (fully or partially) observe the current position in the game graph, which in turn is indicative of their mutual current states. In practice, neither sensing and actuating the environment through physical devices nor data forwarding to and from the controller and signal processing in the controller are instantaneous. The resultant delays force the controller to draw decisions before being aware of the recent history of a play and to submit these decisions well before they can take effect asynchronously. It is known that existence of a winning strategy for the controller in games with such delays is decidable over finite game graphs and with respect to $\omega$-regular objectives. The underlying reduction, however, is impractical for non-trivial delays as it incurs a blow-up of the game graph which is exponential in the magnitude of the delay. For safety objectives, we propose a more practical incremental algorithm successively synthesizing a series of controllers handling increasing delays and reducing the game-graph size in between. It is demonstrated using benchmark examples that even a simplistic explicit-state implementation of this algorithm outperforms state-of-the-art symbolic synthesis algorithms as soon as non-trivial delays have to be handled. We furthermore address the practically relevant cases of non-order-preserving delays and bounded message loss, as arising in actual networked control, thereby considerably extending the scope of regular game theory under delay.
Nonlinear interpolants have been shown useful for the verification of programs and hybrid systems in contexts of theorem proving, model checking, abstract interpretation, etc. The underlying synthesis problem, however, is challenging and existing methods have limitations on the form of formulae to be interpolated. We leverage classification techniques with space transformations and kernel tricks as established in the realm of machine learning, and present a counterexample-guided method named NIL for synthesizing polynomial interpolants, thereby yielding a unified framework tackling the interpolation problem for the general quantifier-free theory of nonlinear arithmetic, possibly involving transcendental functions. We prove the soundness of NIL and propose sufficient conditions under which NIL is guaranteed to converge, i.e., the derived sequence of candidate interpolants converges to an actual interpolant, and is complete, namely the algorithm terminates by producing an interpolant if there exists one. The applicability and effectiveness of our technique are demonstrated experimentally on a collection of representative benchmarks from the literature, where in particular, our method suffices to address more interpolation tasks, including those with perturbations in parameters, and in many cases synthesizes simpler interpolants compared with existing approaches.
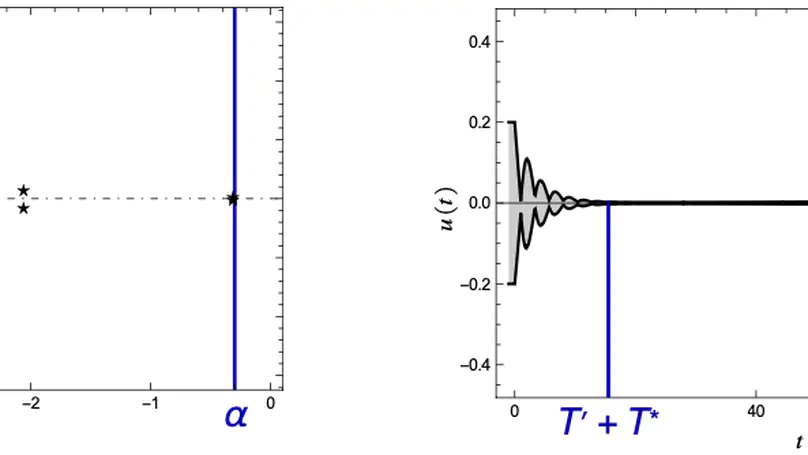
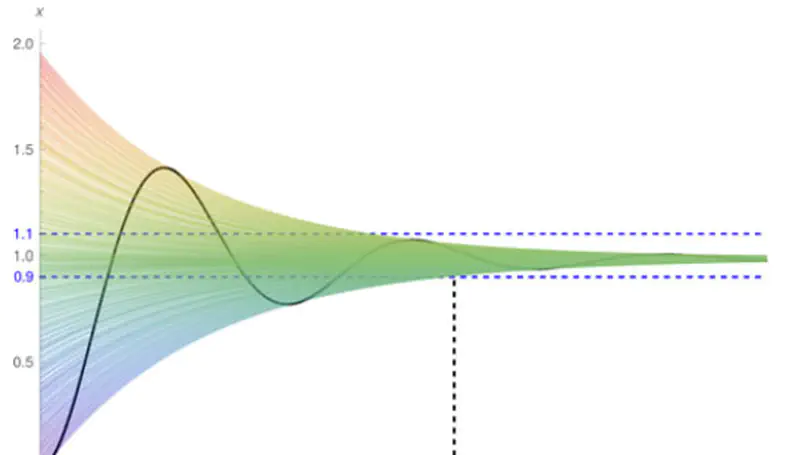
Delayed coupling between state variables occurs regularly in technical dynamical systems, especially embedded control. As it consequently is omnipresent in safety-critical domains, there is an increasing interest in the safety verification of systems modelled by Delay Differential Equations (DDEs). In this paper, we leverage qualitative guarantees for the existence of an exponentially decreasing estimation on the solutions to DDEs as established in classical stability theory, and present a quantitative method for constructing such delay-dependent estimations, thereby facilitating a reduction of the verification problem over an unbounded temporal horizon to a bounded one. Our technique builds on the linearization technique of nonlinear dynamics and spectral analysis of the linearized counterparts. We show experimentally on a set of representative benchmarks from the literature that our technique indeed extends the scope of bounded verification techniques to unbounded verification tasks. Moreover, our technique is easy to implement and can be combined with any automatic tool dedicated to bounded verification of DDEs.
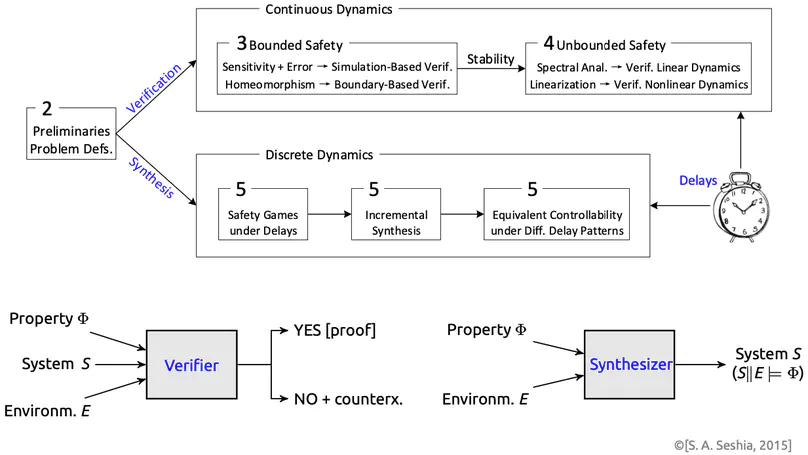
Conventional embedded systems have over the past two decades vividly evolved into an open, interconnected form that integrates capabilities of computing, communication and control, thereby triggering yet another round of global revolution of the information technology. This form, now known as cyber-physical systems, has witnessed an increasing number of safety-critical systems particularly in major scientific projects vital to the national well-being and the people’s livelihood. Prominent examples include automotive electronics, health care, nuclear reactors, high-speed transportations, manned spaceflight, etc., in which a malfunction of any software or hardware component would potentially lead to catastrophic consequences like significant casualties and economic losses. Meanwhile with the rapid development of feedback control, sensor techniques and computer control, time delays have become an essential feature underlying both the continuous evolution of physical plants and the discrete transition of computer programs, which may well annihilate the safety certificate and control performance of embedded systems. Traditional engineering methods, e.g., testing and simulations, are nevertheless argued insufficient for the zero-tolerance of failures incurred in time-delayed systems in a safety-critical context. Therefore, how to rigorously verify and design reliable safety-critical embedded systems involving delays tends to be a grand challenge in computer science and the control community. In contrast to delay-free systems, time-delayed systems yield substantially higher theoretical complexity thus rendering the underlying design and verification tasks significantly harder. This dissertation focuses on the formal verification and controller synthesis of time-delayed dynamical systems, while particularly addressing the safety verification of continuous dynamics governed by delay differential equations and the control-strategy synthesis of discrete dynamics captured by delayed safety games, with applications in a typical set of representative benchmarks from the literature.
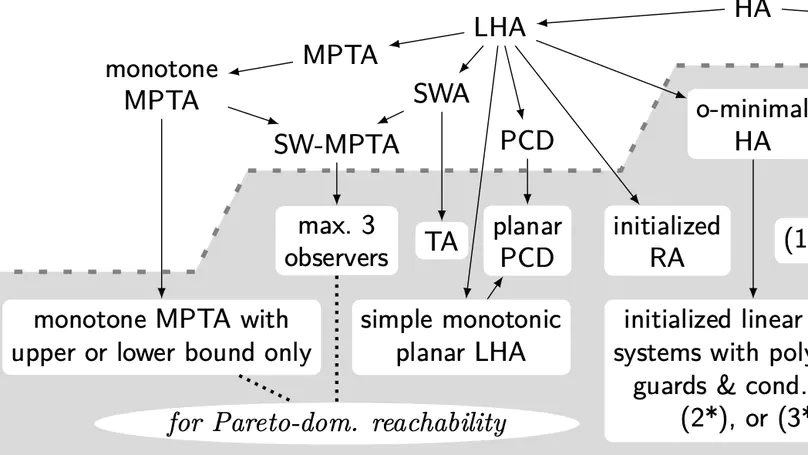
Hybrid automata are an elegant formal model seamlessly integrating differential equations representing continuous dynamics with automata capturing switching behavior. Since the introduction of the computational model more than a quarter of a century ago [Maler et al. 1992], its algorithmic verification has been an area of intense research. Within this note, which is dedicated to Oded Maler (1957–2018) as one of the inventors of the model, we are trying to delineate major lines of attack to the reachability problem for hybrid automata. Due to its relation to system safety, the reachability problem is a prototypical verification problem for hybrid discrete-continuous system dynamics.
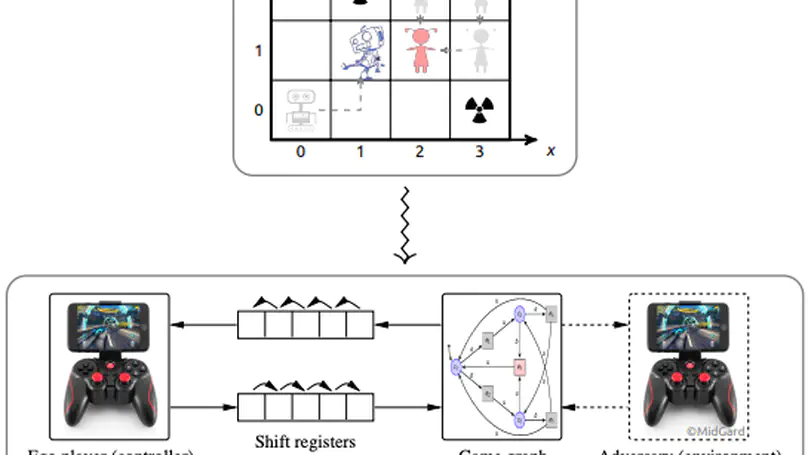
The possible interactions between a controller and its environment can naturally be modelled as the arena of a two-player game, and adding an appropriate winning condition permits to specify desirable behavior. The classical model here is the positional game, where both players can (fully or partially) observe the current position in the game graph, which in turn is indicative of their mutual current states. In practice, neither sensing or actuating the environment through physical devices nor data forwarding to and signal processing in the controller are instantaneous. The resultant delays force the controller to draw decisions before being aware of the recent history of a play. It is known that existence of a winning strategy for the controller in games with such delays is decidable over finite game graphs and with respect to $\omega$-regular objectives. The underlying reduction, however, is impractical for non-trivial delays as it incurs a blow-up of the game graph which is exponential in the magnitude of the delay. For safety objectives, we propose a more practical incremental algorithm synthesizing a series of controllers handling increasing delays and reducing game-graph size in between. It is demonstrated using benchmark examples that even a simplistic explicit-state implementation of this algorithm outperforms state-of-the-art symbolic synthesis algorithms as soon as non-trivial delays have to be handled. We furthermore shed some light on the practically relevant case of non-order-preserving delays, as arising in actual networked control, thereby considerably extending the scope of regular game theory under delay pioneered by Klein and Zimmermann.
The reachability problem is one of the most important issues in the verification of hybrid systems. But unfortunately the reachable sets for most of hybrid systems are not computable. In the literature, only some special families of linear vector fields are proved with decidable reachability problem, let alone nonlinear ones. In this paper, we investigate the reachability problem of nonlinear vector fields by identifying three families of nonlinear vector fields with solvability and prove that their reachability problems are decidable. An $n$-dimension dynamical system is called solvable if its state variables can be partitioned into $m$ groups such that the derivatives of the variables in the $i$th group are linear in themselves, but possibly nonlinear in the variables from the $1$-st to $i-1$th groups. The three families of nonlinear solvable vector fields under consideration are: the matrices corresponding to the linear parts of any vector field in the first family are nilpotent; the matrices corresponding to the linear parts of any vector in the second family are only with real eigenvalues; the matrices corresponding to the linear parts of any vector field in the third family are only with pure imaginary eigenvalues. The experimental results indicate the efficiency of our approach.
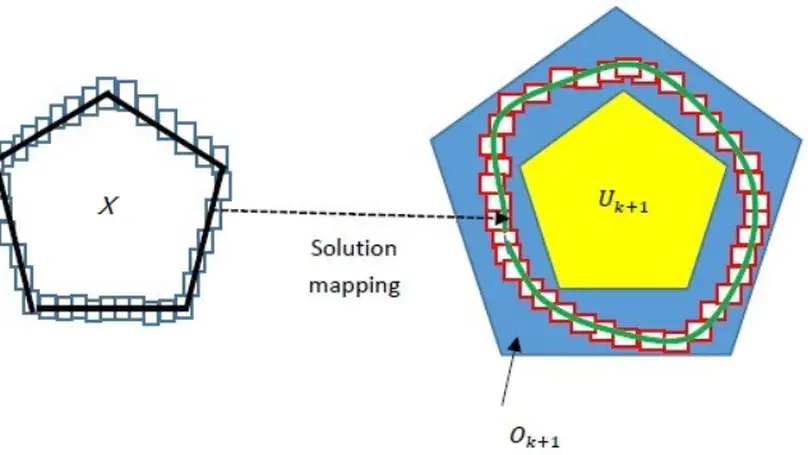
Delays in feedback control loop, as induced by networked distributed control schemes, may have detrimental effects on control performance. This induces an interest in safety verification of delay differential equations (DDEs) used as a model of embedded control. This article explores reachable-set computation for a class of DDEs featuring a local homeomorphism property. This topological property facilitates construction of over- and under-approximations of their full reachable sets by performing reachability analysis on the boundaries of their initial sets, thereby permitting an efficient lifting of reach-set computation methods for ODEs to DDEs. Membership in this class of DDEs is determined by conducting sensitivity analysis of the solution mapping with respect to the initial states to impose a bound constraint on the time-lag term. We then generalize boundary-based reachability analysis to such DDEs. Our reachability algorithm is iterative along the time axis and the computations in each iteration are performed in two steps. The first step computes an enclosure of the set of states reachable from the boundary of the step’s initial state set. The second step derives an over- and under-approximations of the full reachable set by including (excluding, resp.) the obtained boundary enclosure from certain convex combinations of points in that boundary enclosure. Experiments on two illustrative examples demonstrate the efficacy of our algorithm.
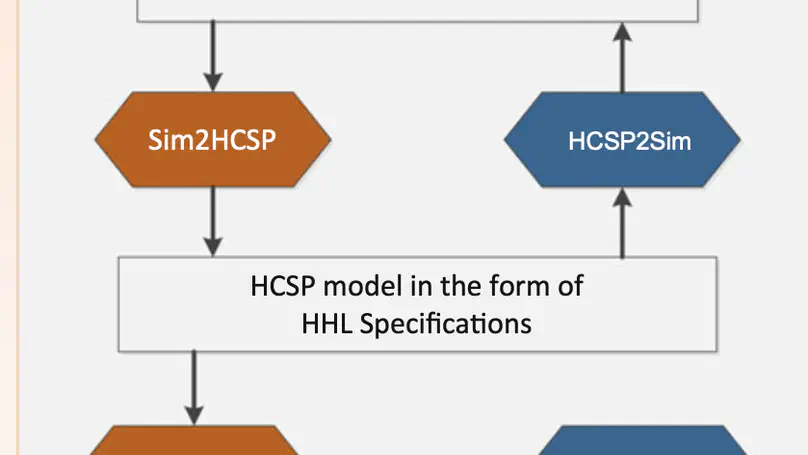
We introduce a toolchain MARS for Modelling, Analyzing and veRifying hybrid Systems we developed in the past years. Using MARS, we build executable models of hybrid systems using the industrial standard environment Simulink/Stateflow, which facilitates analysis by simulation. To complement simulation, formal verification of Simulink/Stateflow models is conducted in the toolchain via the following steps. First, we translate Simulink/Stateflow diagrams to Hybrid CSP (HCSP) processes by an automatic translator Sim2HCSP, where HCSP is an extension of CSP for formally modelling hybrid systems; Second, to justify the translation, another automatic translator HCSP2Sim that translates from HCSP to Simulink is provided, so that the consistency between the original Simulink/Stateflow model and the translated HCSP formal model can be checked by co-simulation; Then, the HCSP processes obtained in the first step are verified by an interactive Hybrid Hoare Logic (HHL) prover; During the verification, an invariant generator independent of the theorem prover for synthesizing invariants for differential equations and loops is needed. We demonstrate the toolchain by analysis and verification of a descent guidance control program of a lunar lander, which is a real-world industry example.
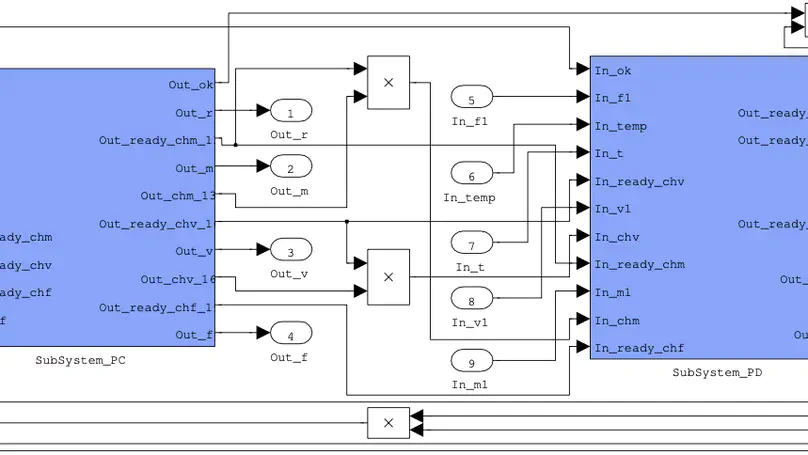
It is well known that informal simulation-based design of embedded systems has a low initial cost and delivers early results; yet it cannot guarantee the correctness and reliability of the system to be developed. In contrast, the correctness and reliability of the system can be thoroughly investigated with formal design, but it requires a larger effort, which increases the development cost. Therefore, it is desirable for a designer to move between formal and informal design. This paper describes how to translate Hybrid CSP (HCSP) formal models into Simulink graphical models, so that the models can be simulated and tested using a MATLAB platform, thus avoiding expensive formal verification if the development is at a stage where it is considered unnecessary. Together with our previous work on encoding Simulink/Stateflow diagrams into HCSP, it provides a two-way path in the design of embedded systems, so that the designer can flexibly shift between formal and informal models. The translation from HCSP into Simulink diagrams is implemented as a fully automatic tool, and the correctness of the translation is justified using Unifying Theories of Programming (UTP).
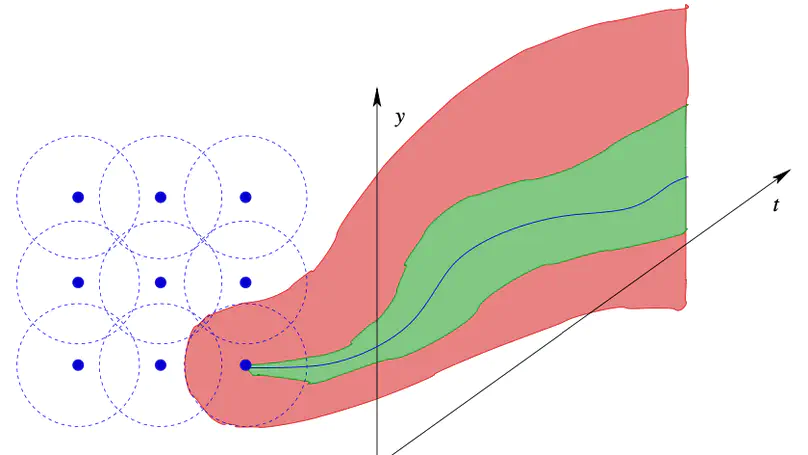
Verification by simulation, based on covering the set of time-bounded trajectories of a dynamical system evolving from the initial state set by means of a finite sample of initial states plus a sensitivity argument, has recently attracted interest due to the availability of powerful simulators for rich classes of dynamical systems. System models addressed by such techniques involve ordinary differential equations (ODEs) and can readily be extended to delay differential equations (DDEs). In doing so, the lack of validated solvers for DDEs, however, enforces the use of numeric approximations such that the resulting verification procedures would have to resort to (rather strong) assumptions on numerical accuracy of the underlying simulators, which lack formal validation or proof. In this paper, we pursue a closer integration of the numeric solving and the sensitivity-related state bloating algorithms underlying verification by simulation, together yielding a safe enclosure algorithm for DDEs suitable for use in automated formal verification. The key ingredient is an on-the-fly computation of piecewise linear, local error bounds by nonlinear optimization, with the error bounds uniformly covering sensitivity information concerning initial states as well as integration error.
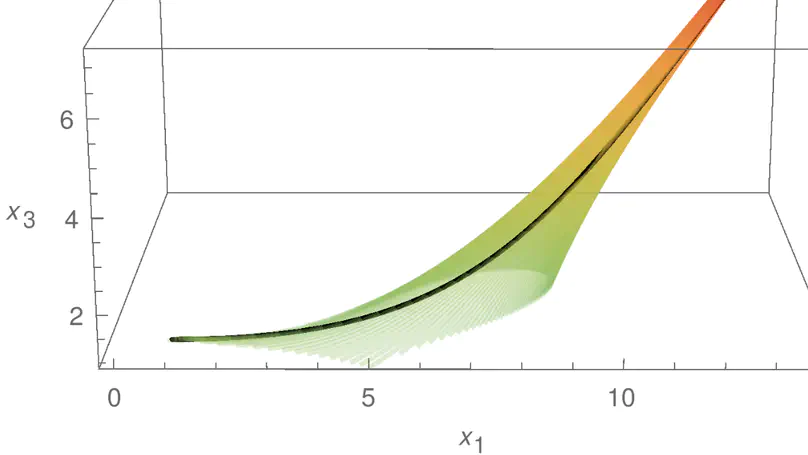
The reachability problem is one of the most important issues in the verification of hybrid systems. But unfortunately the reachable sets for most of hybrid systems are not computable except for some special families. In our previous work, we identified a family of vector fields, whose state parts are linear with real eigenvalues, while input parts are exponential functions, and proved its reachability problem is decidable. In this paper, we investigate another family of vector fields, whose state parts are linear, but with pure imagine eigenvalues, while input parts are trigonometric functions, and prove its reachability problem is decidable also. To the best of our knowledge, the two families are the largest families of linear vector fields with a decidable reachability problem. In addition, we present an approach on how to abstract general linear dynamical systems to the first family. Comparing with existing abstractions for linear dynamical systems, experimental results indicate that our abstraction is more precise.
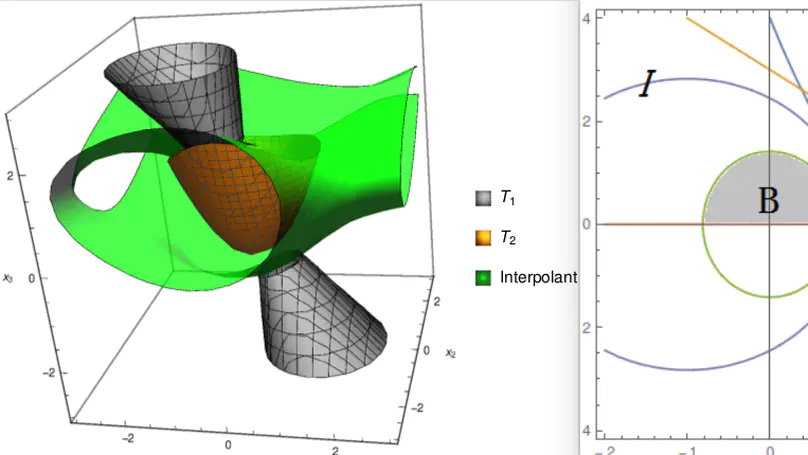
An algorithm for generating interpolants for formulas which are conjunctions of quadratic polynomial inequalities (both strict and nonstrict) is proposed. The algorithm is based on a key observation that quadratic polynomial inequalities can be linearized if they are concave. A generalization of Motzkin’s transposition theorem is proved, which is used to generate an interpolant between two mutually contradictory conjunctions of polynomial inequalities, using semi-definite programming in time complexity $\mathcal{O}(n^3+nm)$, where $n$ is the number of variables and $m$ is the number of inequalities (this complexity analysis assumes that despite the numerical nature of approximate SDP algorithms, they are able to generate correct answers in a fixed number of calls). Using the framework proposed by Sofronie-Stokkermans for combining interpolants for a combination of quantifier-free theories which have their own interpolation algorithms, a combination algorithm is given for the combined theory of concave quadratic polynomial inequalities and the equality theory over uninterpreted functions.
The reachability problem is one of the most important issues in the verification of hybrid systems. Computing the reachable sets of differential equations is difficult, although computing the reachable sets of finite state machines is well developed. Hence, it is not surprising that the reachability of most of hybrid systems is undecidable. In this paper, we identify a family of vector fields and show its reachability problem is decidable. The family consists of all vector fields whose state parts are linear, while input parts are non-linear, possibly with exponential expressions. Such vector fields are commonly used in practice.To the best of our knowledge, the family is one of the most expressive families of vector fields with a decidable reachability problem.The decidability is achieved by proving the decidability of the extension of Tarski’s algebra with some specific exponential functions, which has been proved by Strzeboński. In this paper, we propose another decision procedure, which is more efficient when all constraints are open sets. The experimental results indicate the efficiency of our approach, even better than existing approaches based on approximation and numeric computation in general.