College of Computer Science and Technology
Zhejiang University
Formal Verification Group
The Formal Verification Group (FICTION1), headed by Prof. Dr. Mingshuai Chen, is a research unit embedded in the College of Computer Science and Technology at Zhejiang University (ZJU), Hangzhou, China. We develop formal reasoning techniques for programs and hybrid discrete-continuous systems for ensuring the reliability and effectiveness of safety-critical software systems while pushing the limits of automation as far as possible. Check out the featured publications as examples of our research.
We are constantly on the hunt of self-motivated Postdocs, Ph.D./Master Students, and Research Assistants/Interns to join our group at ZJU. Check out the open positions in case you are interested.
-
FICTION (/ˈfɪkʃn/) refers to any creative work that may deviate from plausibility. ↩︎
Featured Publications
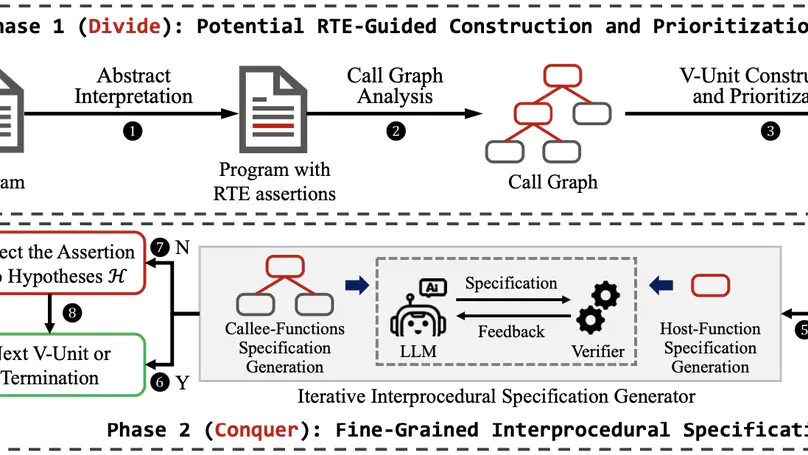
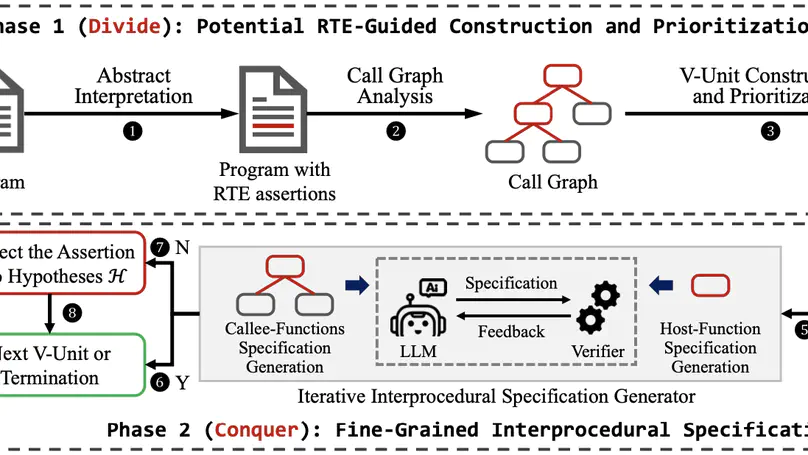
Fully automated verification of large-scale software and hardware systems is arguably the holy grail of formal methods. Large language models (LLMs) have recently demonstrated their potential for enhancing the degree of automation in formal verification by, e.g., generating formal specifications as essential to deductive verification, yet exhibit poor scalability due to context-length limitations and, more importantly, the difficulty of inferring complex, interprocedural specifications. This paper presents Preguss – a modular, fine-grained framework for automating the generation and refinement of formal specifications. Preguss synergizes between static analysis and deductive verification by steering two components in a divide-and-conquer fashion: (i) potential runtime error-guided construction and prioritization of verification units, and (ii) LLM-aided synthesis of interprocedural specifications at the unit level. We show that Preguss substantially outperforms state-of-the-art LLM-based approaches and, in particular, it enables highly automated RTE-freeness verification for real-world programs with over a thousand LoC, with a reduction of 80.6%$\sim$88.9% human verification effort.
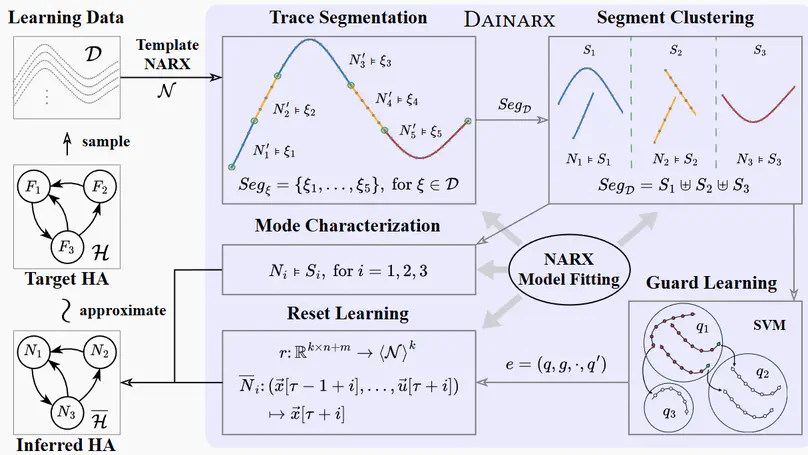
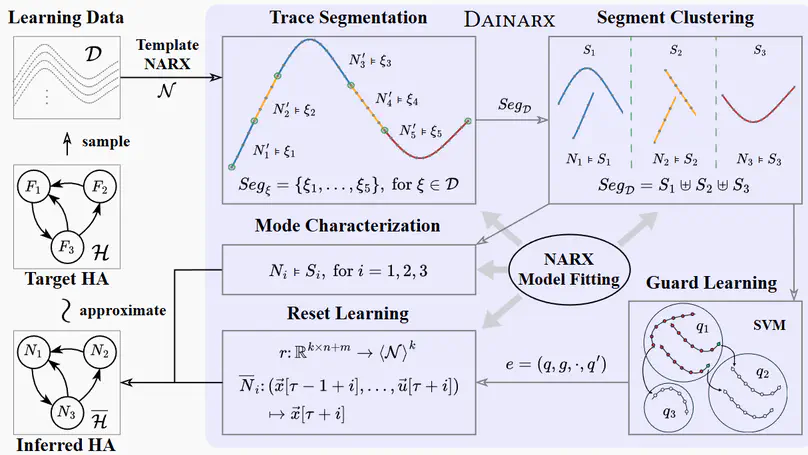
This paper addresses the problem of inferring hybrid automata from input-output traces of hybrid systems exhibiting discrete mode switches between continuously evolving dynamics. Existing approaches primarily rely on derivative-based strategies in which (i) mode switches are detected by drastic variations in derivatives and (ii) trace segments are clustered based on signal similarity – both requiring user-supplied thresholds. We present a derivative-agnostic approach, named Dainarx, for inferring nonlinear hybrid systems whose dynamics are captured by nonlinear autoregressive exogenous (NARX) models. Dainarx employs NARX models as a unified, threshold-free representation for both mode switching and segment clustering. We show that Dainarx suffices to learn models that closely approximate a general class of hybrid systems featuring high-order nonlinear dynamics with exogenous inputs, nonlinear guard conditions, linear resets, and noise. Experimental results on a collection of benchmarks demonstrate that our approach effectively and efficiently infers nontrivial hybrid automata with high-order dynamics, yielding significantly more accurate approximations than state-of-the-art techniques, while achieving robustness comparable to approaches dedicated to fitting noisy data.
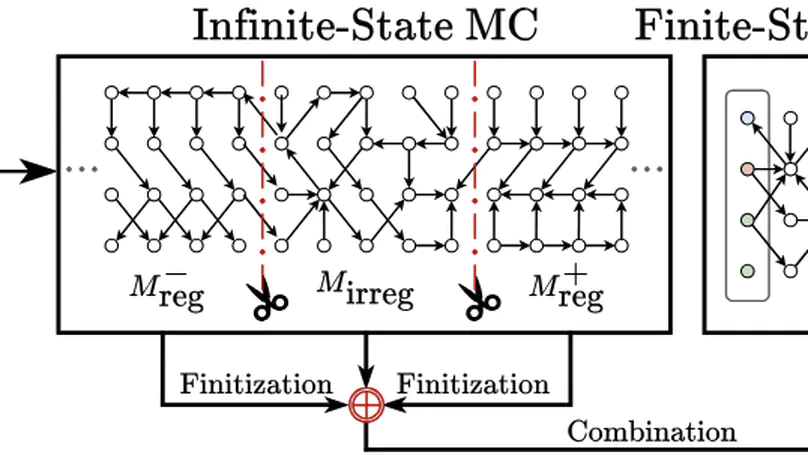
This paper introduces $k$-d PCPs – the class of probabilistic counter programs with $k \in \mathbb{N}$ counter variables inducing possibly infinite-state Markov chains. We show that the universal (positive) almost-sure termination problem is undecidable for $k$-d PCPs in general, yet decidable for $1$-d PCPs. We present an efficient decision procedure for the latter leveraging the technique of Markov chain finitization. Moreover, we identify several classes of $k$-d PCPs that are reducible to $1$-d PCPs – thus their termination properties can be inferred automatically. Experiments demonstrate that our decision procedure can certify (positive) almost-sure termination – without resorting to invariants or supermartingales – of non-trivial probabilistic programs beyond the scope of existing tools.
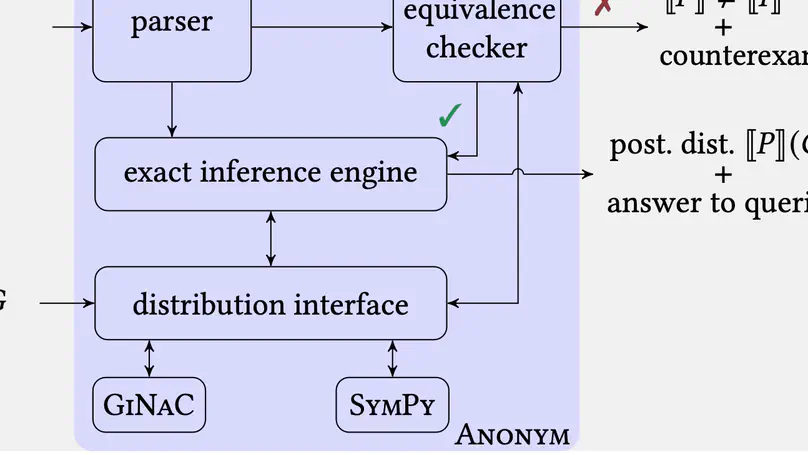
We present an exact Bayesian inference method for inferring posterior distributions encoded by probabilistic programs featuring possibly unbounded loops. Our method is built on a denotational semantics represented by probability generating functions, which resolves semantic intricacies induced by intertwining discrete probabilistic loops with conditioning (for encoding posterior observations). We implement our method in a tool called Prodigy; it augments existing computer algebra systems with the theory of generating functions for the (semi-)automatic inference and quantitative verification of conditioned probabilistic programs. Experimental results show that Prodigy can handle various infinite-state loopy programs and exhibits comparable performance to state-of-the-art exact inference tools over loop-free benchmarks.
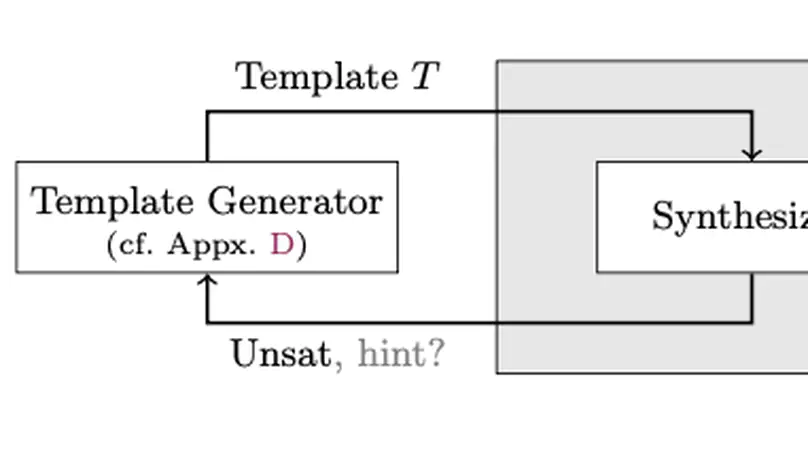
Essential tasks for the verification of probabilistic programs include bounding expected outcomes and proving termination in finite expected runtime. We contribute a simple yet effective inductive synthesis approach for proving such quantitative reachability properties by generating inductive invariants on source-code level. Our implementation shows promise: It finds invariants for (in)finite-state programs, can beat state-of-the-art probabilistic model checkers, and is competitive with modern tools dedicated to invariant synthesis and expected runtime reasoning.
We present a new proof rule for verifying lower bounds on quantities of probabilistic programs. Our proof rule is not confined to almost-surely terminating programs – as is the case for existing rules – and can be used to establish non-trivial lower bounds on, e.g., termination probabilities and expected values, for possibly divergent probabilistic loops, e.g., the well-known three-dimensional random walk on a lattice.
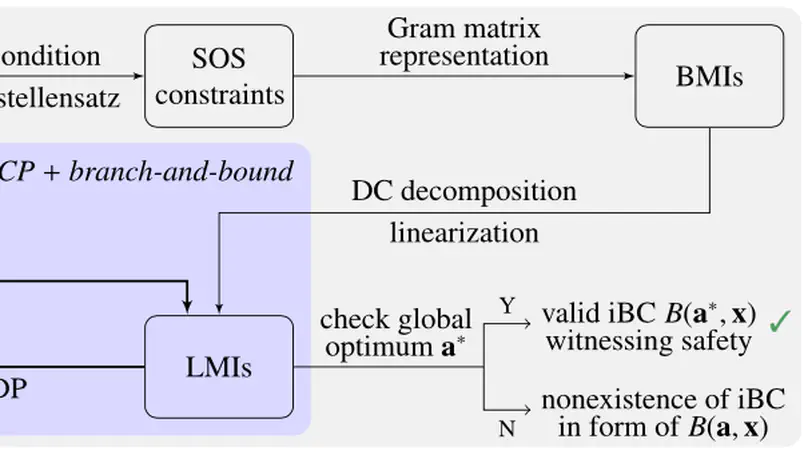
We present the invariant barrier-certificate condition that witnesses unbounded-time safety of differential dynamical systems. The proposed condition is the weakest possible one to attain inductive invariance. We show that discharging the invariant barrier-certificate condition —thereby synthesizing invariant barrier certificates— can be encoded as solving an optimization problem subject to bilinear matrix inequalities (BMIs). We further propose a synthesis algorithm based on difference-of-convex programming, which approaches a local optimum of the BMI problem via solving a series of convex optimization problems. This algorithm is incorporated in a branch-and-bound framework that searches for the global optimum in a divide-and-conquer fashion. We present a weak completeness result of our method, namely, a barrier certificate is guaranteed to be found (under some mild assumptions) whenever there exists an inductive invariant (in the form of a given template) that suffices to certify safety. Experimental results on benchmarks demonstrate the effectiveness and efficiency of our approach.

We study discrete probabilistic programs with potentially unbounded looping behaviors over an infinite state space. We present, to the best of our knowledge, the first decidability result for the problem of determining whether such a program generates exactly a specified distribution over its outputs (provided the program terminates almost-surely). The class of distributions that can be specified in our formalism consists of standard distributions (geometric, uniform, etc.) and finite convolutions thereof. Our method relies on representing these (possibly infinite-support) distributions as probability generating functions which admit effective arithmetic operations. We have automated our techniques in a tool called Prodigy, which supports automatic invariance checking, compositional reasoning of nested loops, and efficient queries to the output distribution, as demonstrated by experiments.
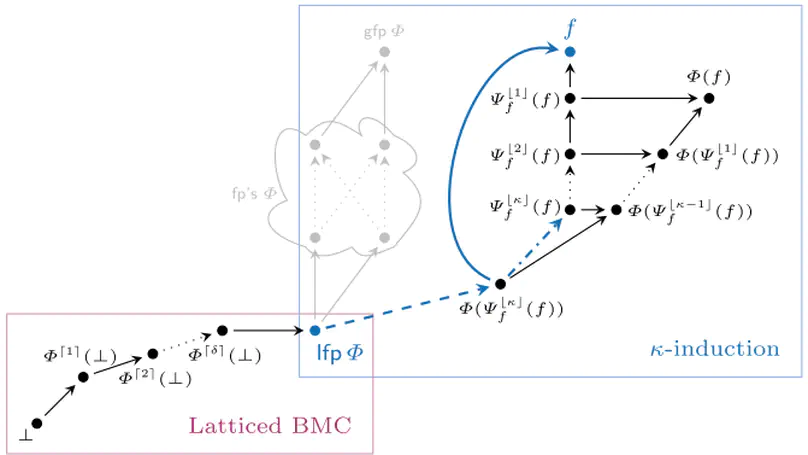
We revisit two well-established verification techniques, $k$-induction and bounded model checking (BMC), in the more general setting of fixed point theory over complete lattices. Our main theoretical contribution is latticed $k$-induction, which (i) generalizes classical $k$-induction for verifying transition systems, (ii) generalizes Park induction for bounding fixed points of monotonic maps on complete lattices, and (iii) extends from naturals $k$ to transfinite ordinals $\kappa$, thus yielding $\kappa$-induction. The lattice-theoretic understanding of $k$-induction and BMC enables us to apply both techniques to the fully automatic verification of infinite-state probabilistic programs. Our prototypical implementation manages to automatically verify non-trivial specifications for probabilistic programs taken from the literature that – using existing techniques – cannot be verified without synthesizing a stronger inductive invariant first.
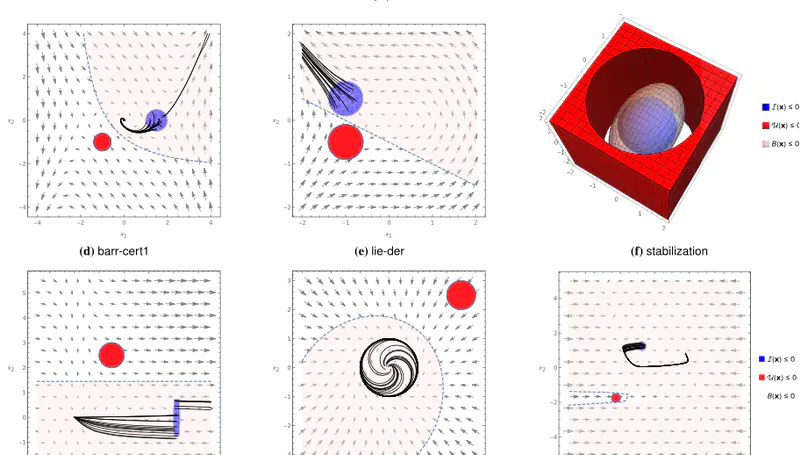
A barrier certificate often serves as an inductive invariant that isolates an unsafe region from the reachable set of states, and hence is widely used in proving safety of hybrid systems possibly over the infinite time horizon. We present a novel condition on barrier certificates, termed the invariant barrier-certificate condition, that witnesses unbounded-time safety of differential dynamical systems. The proposed condition is by far the least conservative one on barrier certificates, and can be shown as the weakest possible one to attain inductive invariance. We show that discharging the invariant barrier-certificate condition—thereby synthesizing invariant barrier certificates—can be encoded as solving an optimization problem subject to bilinear matrix inequalities (BMIs). We further propose a synthesis algorithm based on difference-of-convex programming, which approaches a local optimum of the BMI problem via solving a series of convex optimization problems. This algorithm is incorporated in a branch-and-bound framework that searches for the global optimum in a divide-and-conquer fashion. We present a weak completeness result of our method, in the sense that a barrier certificate is guaranteed to be found (under some mild assumptions) whenever there exists an inductive invariant (in the form of a given template) that suffices to certify safety of the system. Experimental results on benchmark examples demonstrate the effectiveness and efficiency of our approach.

In this paper, we propose a method for bounding the probability that a stochastic differential equation (SDE) system violates a safety specification over the infinite time horizon. SDEs are mathematical models of stochastic processes that capture how states evolve continuously in time. They are widely used in numerous applications such as engineered systems (e.g., modeling how pedestrians move in an intersection), computational finance (e.g., modeling stock option prices), and ecological processes (e.g., population change over time). Previously the safety verification problem has been tackled over finite and infinite time horizons using a diverse set of approaches. The approach in this paper attempts to connect the two views by first identifying a finite time bound, beyond which the probability of a safety violation can be bounded by a negligibly small number. This is achieved by discovering an exponential barrier certificate that proves exponentially converging bounds on the probability of safety violations over time. Once the finite time interval is found, a finite-time verification approach is used to bound the probability of violation over this interval. We demonstrate our approach over a collection of interesting examples from the literature, wherein our approach can be used to find tight bounds on the violation probability of safety properties over the infinite time horizon.
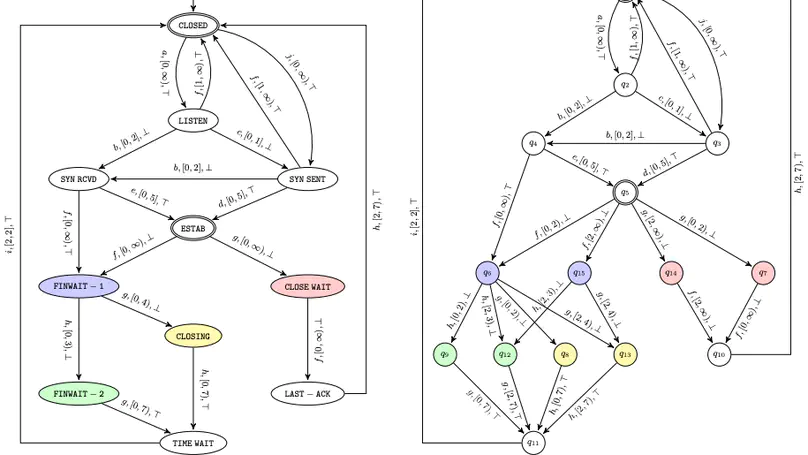
We present an algorithm for active learning of deterministic timed automata with a single clock. The algorithm is within the framework of Angluin’s $L^*$ algorithm and inspired by existing work on the active learning of symbolic automata. Due to the need of guessing for each transition whether it resets the clock, the algorithm is of exponential complexity in the size of the learned automata. Before presenting this algorithm, we propose a simpler version where the teacher is assumed to be smart in the sense of being able to provide the reset information. We show that this simpler setting yields a polynomial complexity of the learning process. Both of the algorithms are implemented and evaluated on a collection of randomly generated examples. We furthermore demonstrate the simpler algorithm on the functional specification of the TCP protocol.
Contact
- Wensan Road 232, Hangzhou, Zhejiang 310012
- Room 510, East Building, North Park, Xixi Campus
- GitHub Contact
- Zoom Us