Does a Program Yield the Right Distribution?

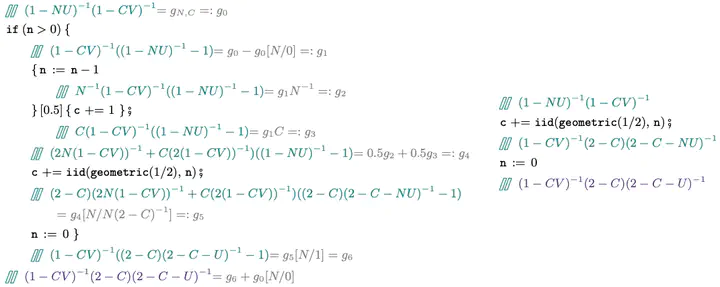
Abstract

We study discrete probabilistic programs with potentially unbounded looping behaviors over an infinite state space. We present, to the best of our knowledge, the first decidability result for the problem of determining whether such a program generates exactly a specified distribution over its outputs (provided the program terminates almost-surely). The class of distributions that can be specified in our formalism consists of standard distributions (geometric, uniform, etc.) and finite convolutions thereof. Our method relies on representing these (possibly infinite-support) distributions as probability generating functions which admit effective arithmetic operations. We have automated our techniques in a tool called Prodigy, which supports automatic invariance checking, compositional reasoning of nested loops, and efficient queries to the output distribution, as demonstrated by experiments.