Synthesizing Invariant Barrier Certificates via Difference-of-Convex Programming
Abstract
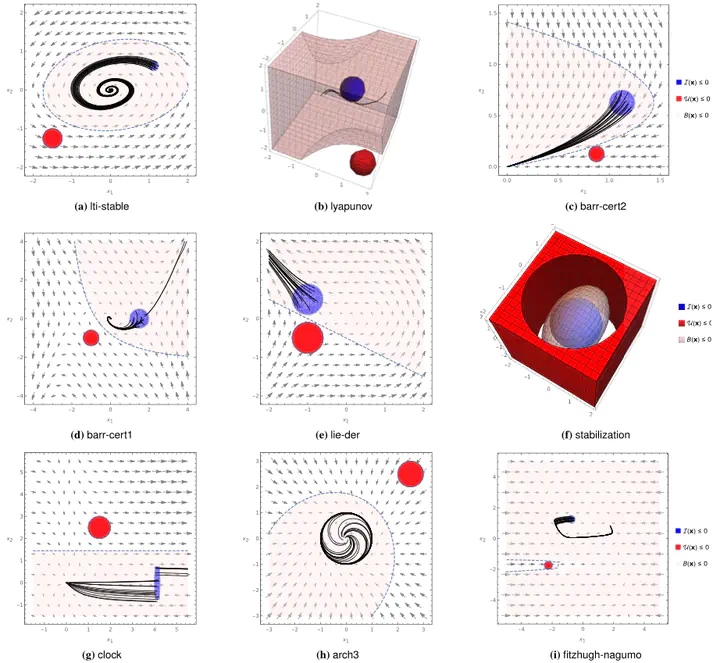
A barrier certificate often serves as an inductive invariant that isolates an unsafe region from the reachable set of states, and hence is widely used in proving safety of hybrid systems possibly over the infinite time horizon. We present a novel condition on barrier certificates, termed the invariant barrier-certificate condition, that witnesses unbounded-time safety of differential dynamical systems. The proposed condition is by far the least conservative one on barrier certificates, and can be shown as the weakest possible one to attain inductive invariance. We show that discharging the invariant barrier-certificate condition—thereby synthesizing invariant barrier certificates—can be encoded as solving an optimization problem subject to bilinear matrix inequalities (BMIs). We further propose a synthesis algorithm based on difference-of-convex programming, which approaches a local optimum of the BMI problem via solving a series of convex optimization problems. This algorithm is incorporated in a branch-and-bound framework that searches for the global optimum in a divide-and-conquer fashion. We present a weak completeness result of our method, in the sense that a barrier certificate is guaranteed to be found (under some mild assumptions) whenever there exists an inductive invariant (in the form of a given template) that suffices to certify safety of the system. Experimental results on benchmark examples demonstrate the effectiveness and efficiency of our approach.