Latticed $k$-Induction with an Application to Probabilistic Programs

Abstract

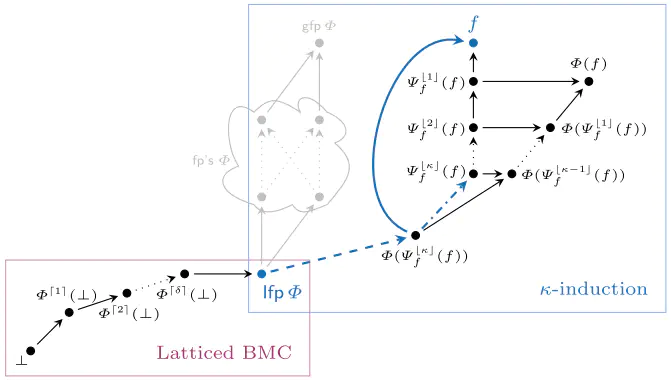
We revisit two well-established verification techniques, $k$-induction and bounded model checking (BMC), in the more general setting of fixed point theory over complete lattices. Our main theoretical contribution is latticed $k$-induction, which (i) generalizes classical $k$-induction for verifying transition systems, (ii) generalizes Park induction for bounding fixed points of monotonic maps on complete lattices, and (iii) extends from naturals $k$ to transfinite ordinals $\kappa$, thus yielding $\kappa$-induction. The lattice-theoretic understanding of $k$-induction and BMC enables us to apply both techniques to the fully automatic verification of infinite-state probabilistic programs. Our prototypical implementation manages to automatically verify non-trivial specifications for probabilistic programs taken from the literature that – using existing techniques – cannot be verified without synthesizing a stronger inductive invariant first.