NIL: Learning Nonlinear Interpolants

Abstract

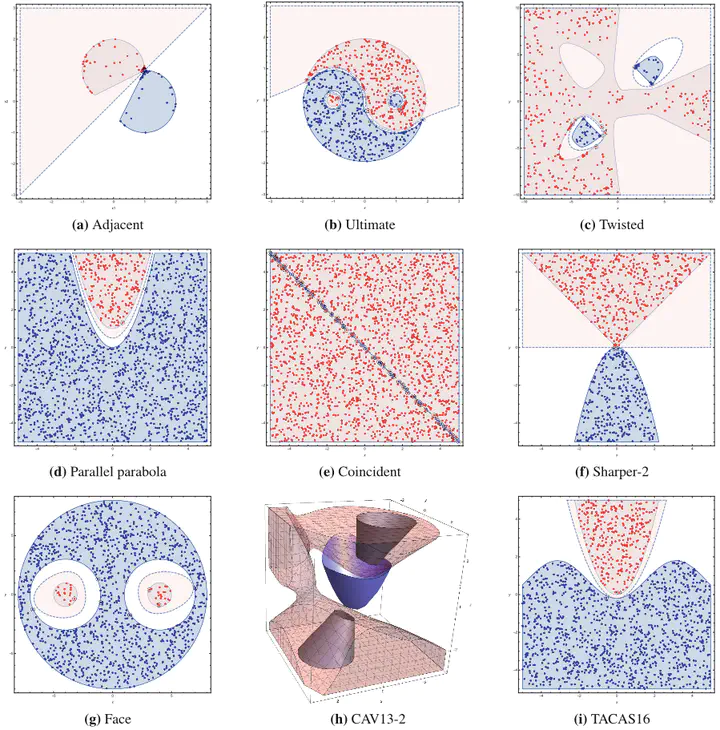
Nonlinear interpolants have been shown useful for the verification of programs and hybrid systems in contexts of theorem proving, model checking, abstract interpretation, etc. The underlying synthesis problem, however, is challenging and existing methods have limitations on the form of formulae to be interpolated. We leverage classification techniques with space transformations and kernel tricks as established in the realm of machine learning, and present a counterexample-guided method named NIL for synthesizing polynomial interpolants, thereby yielding a unified framework tackling the interpolation problem for the general quantifier-free theory of nonlinear arithmetic, possibly involving transcendental functions. We prove the soundness of NIL and propose sufficient conditions under which NIL is guaranteed to converge, i.e., the derived sequence of candidate interpolants converges to an actual interpolant, and is complete, namely the algorithm terminates by producing an interpolant if there exists one. The applicability and effectiveness of our technique are demonstrated experimentally on a collection of representative benchmarks from the literature, where in particular, our method suffices to address more interpolation tasks, including those with perturbations in parameters, and in many cases synthesizes simpler interpolants compared with existing approaches.