Interpolant Synthesis for Quadratic Polynomial Inequalities and Combination with EUF

Abstract

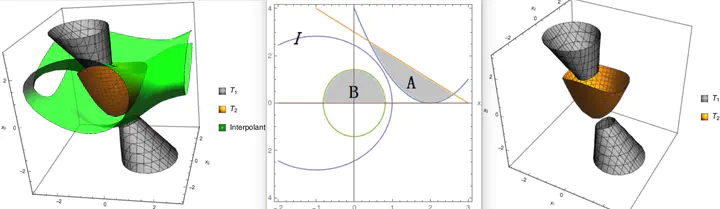
An algorithm for generating interpolants for formulas which are conjunctions of quadratic polynomial inequalities (both strict and nonstrict) is proposed. The algorithm is based on a key observation that quadratic polynomial inequalities can be linearized if they are concave. A generalization of Motzkin’s transposition theorem is proved, which is used to generate an interpolant between two mutually contradictory conjunctions of polynomial inequalities, using semi-definite programming in time complexity $\mathcal{O}(n^3+nm)$, where $n$ is the number of variables and $m$ is the number of inequalities (this complexity analysis assumes that despite the numerical nature of approximate SDP algorithms, they are able to generate correct answers in a fixed number of calls). Using the framework proposed by Sofronie-Stokkermans for combining interpolants for a combination of quantifier-free theories which have their own interpolation algorithms, a combination algorithm is given for the combined theory of concave quadratic polynomial inequalities and the equality theory over uninterpreted functions.