Reachability Analysis for Solvable Dynamical Systems

Abstract

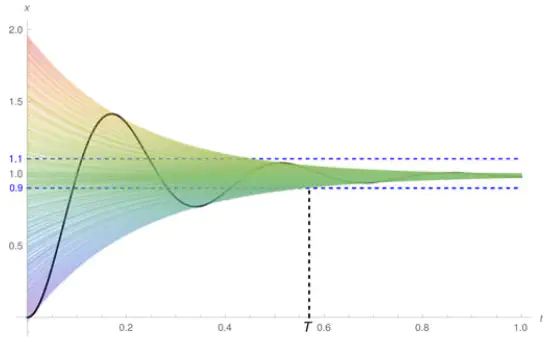
The reachability problem is one of the most important issues in the verification of hybrid systems. But unfortunately the reachable sets for most of hybrid systems are not computable. In the literature, only some special families of linear vector fields are proved with decidable reachability problem, let alone nonlinear ones. In this paper, we investigate the reachability problem of nonlinear vector fields by identifying three families of nonlinear vector fields with solvability and prove that their reachability problems are decidable. An $n$-dimension dynamical system is called solvable if its state variables can be partitioned into $m$ groups such that the derivatives of the variables in the $i$th group are linear in themselves, but possibly nonlinear in the variables from the $1$-st to $i-1$th groups. The three families of nonlinear solvable vector fields under consideration are: the matrices corresponding to the linear parts of any vector field in the first family are nilpotent; the matrices corresponding to the linear parts of any vector in the second family are only with real eigenvalues; the matrices corresponding to the linear parts of any vector field in the third family are only with pure imaginary eigenvalues. The experimental results indicate the efficiency of our approach.