Safe Over- and Under-Approximation of Reachable Sets for Delay Differential Equations

Abstract

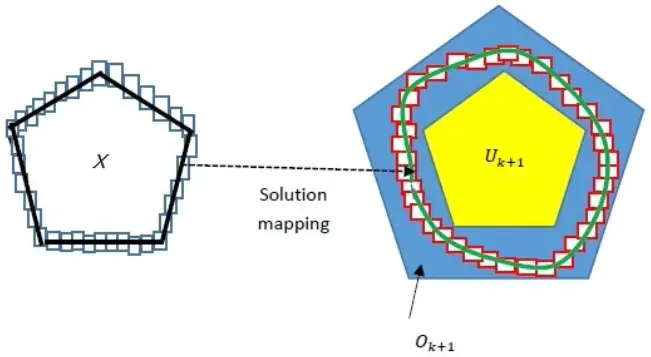
Delays in feedback control loop, as induced by networked distributed control schemes, may have detrimental effects on control performance. This induces an interest in safety verification of delay differential equations (DDEs) used as a model of embedded control. This article explores reachable-set computation for a class of DDEs featuring a local homeomorphism property. This topological property facilitates construction of over- and under-approximations of their full reachable sets by performing reachability analysis on the boundaries of their initial sets, thereby permitting an efficient lifting of reach-set computation methods for ODEs to DDEs. Membership in this class of DDEs is determined by conducting sensitivity analysis of the solution mapping with respect to the initial states to impose a bound constraint on the time-lag term. We then generalize boundary-based reachability analysis to such DDEs. Our reachability algorithm is iterative along the time axis and the computations in each iteration are performed in two steps. The first step computes an enclosure of the set of states reachable from the boundary of the step’s initial state set. The second step derives an over- and under-approximations of the full reachable set by including (excluding, resp.) the obtained boundary enclosure from certain convex combinations of points in that boundary enclosure. Experiments on two illustrative examples demonstrate the efficacy of our algorithm.