Validated Simulation-Based Verification of Delayed Differential Dynamics

Abstract

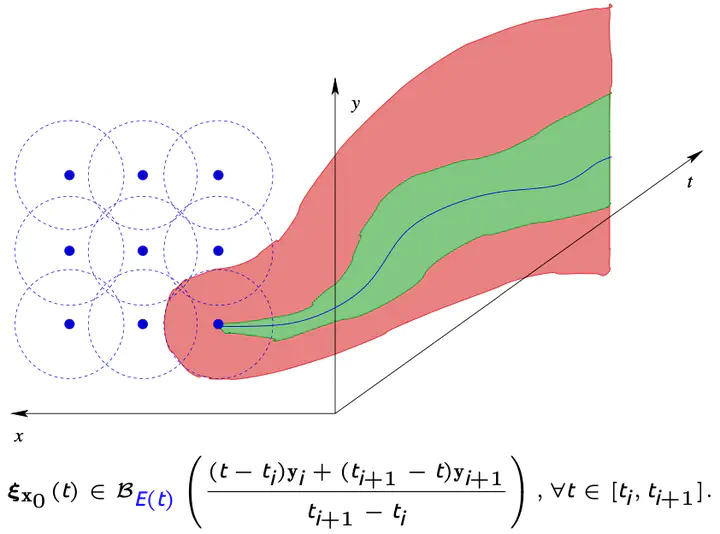
Verification by simulation, based on covering the set of time-bounded trajectories of a dynamical system evolving from the initial state set by means of a finite sample of initial states plus a sensitivity argument, has recently attracted interest due to the availability of powerful simulators for rich classes of dynamical systems. System models addressed by such techniques involve ordinary differential equations (ODEs) and can readily be extended to delay differential equations (DDEs). In doing so, the lack of validated solvers for DDEs, however, enforces the use of numeric approximations such that the resulting verification procedures would have to resort to (rather strong) assumptions on numerical accuracy of the underlying simulators, which lack formal validation or proof. In this paper, we pursue a closer integration of the numeric solving and the sensitivity-related state bloating algorithms underlying verification by simulation, together yielding a safe enclosure algorithm for DDEs suitable for use in automated formal verification. The key ingredient is an on-the-fly computation of piecewise linear, local error bounds by nonlinear optimization, with the error bounds uniformly covering sensitivity information concerning initial states as well as integration error.