On Termination of Polynomial Programs with Equality Conditions

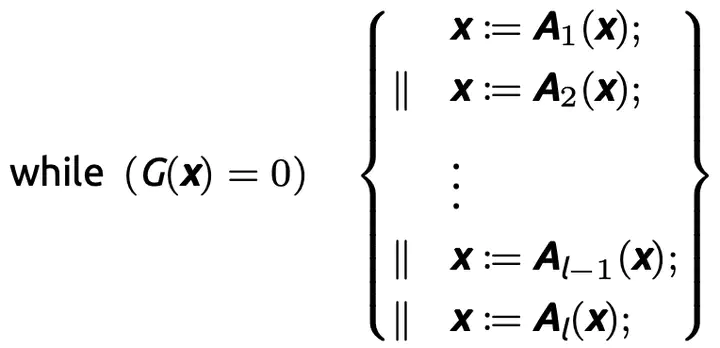
Abstract

We investigate the termination problem of a family of multi-path polynomial programs (MPPs), in which all assignments to program variables are polynomials, and test conditions of loops and conditional statements are polynomial equalities. We show that the set of non-terminating inputs (NTI) of such a program is algorithmically computable, thus leading to the decidability of its termination. To the best of our knowledge, the considered family of MPPs is hitherto the largest one for which termination is decidable. We present an explicit recursive function which is essentially Ackermannian, to compute the maximal length of ascending chains of polynomial ideals under a control function, and thereby obtain a complete answer to the questions raised by Seidenberg. This maximal length facilitates a precise complexity analysis of our algorithms for computing the NTI and deciding termination of MPPs. We extend our method to programs with polynomial guarded commands and show how an incomplete procedure for MPPs with inequality guards can be obtained. An application of our techniques to invariant generation of polynomial programs is further presented.