Derivative-Agnostic Inference of Nonlinear Hybrid Systems

Abstract

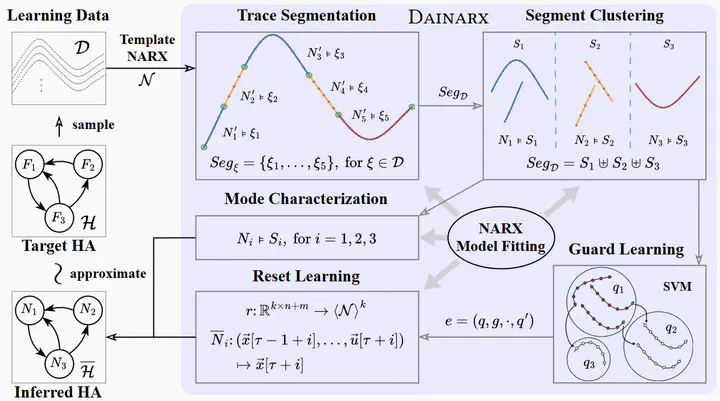
This paper addresses the problem of inferring hybrid automata from input-output traces of hybrid systems exhibiting discrete mode switches between continuously evolving dynamics. Existing approaches primarily rely on derivative-based strategies in which (i) mode switches are detected by drastic variations in derivatives and (ii) trace segments are clustered based on signal similarity – both requiring user-supplied thresholds. We present a derivative-agnostic approach, named Dainarx, for inferring nonlinear hybrid systems whose dynamics are captured by nonlinear autoregressive exogenous (NARX) models. Dainarx employs NARX models as a unified, threshold-free representation for both mode switching and segment clustering. We show that Dainarx suffices to learn models that closely approximate a general class of hybrid systems featuring high-order nonlinear dynamics with exogenous inputs, nonlinear guard conditions, linear resets, and noise. Experimental results on a collection of benchmarks demonstrate that our approach effectively and efficiently infers nontrivial hybrid automata with high-order dynamics, yielding significantly more accurate approximations than state-of-the-art techniques, while achieving robustness comparable to approaches dedicated to fitting noisy data.