On the Almost-Sure Termination of Probabilistic Counter Programs

Abstract

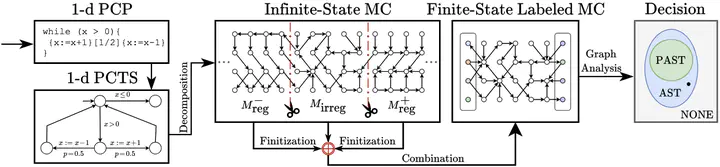
This paper introduces $k$-d PCPs – the class of probabilistic counter programs with $k \in \mathbb{N}$ counter variables inducing possibly infinite-state Markov chains. We show that the universal (positive) almost-sure termination problem is undecidable for $k$-d PCPs in general, yet decidable for $1$-d PCPs. We present an efficient decision procedure for the latter leveraging the technique of Markov chain finitization. Moreover, we identify several classes of $k$-d PCPs that are reducible to $1$-d PCPs – thus their termination properties can be inferred automatically. Experiments demonstrate that our decision procedure can certify (positive) almost-sure termination – without resorting to invariants or supermartingales – of non-trivial probabilistic programs beyond the scope of existing tools.