Learning One-Clock Timed Automata

Abstract

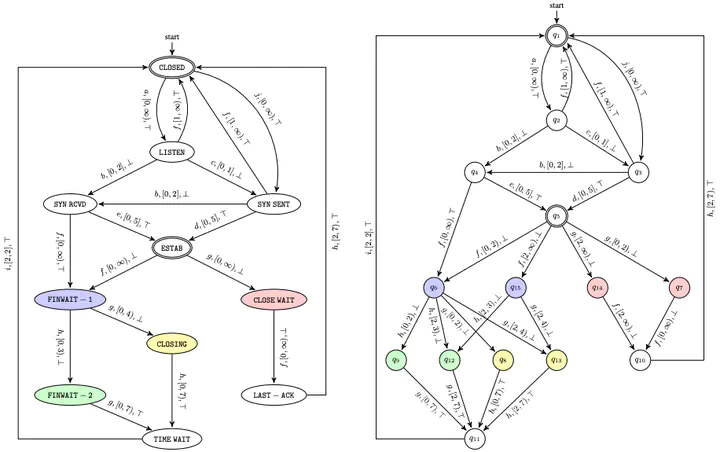
We present an algorithm for active learning of deterministic timed automata with a single clock. The algorithm is within the framework of Angluin’s $L^*$ algorithm and inspired by existing work on the active learning of symbolic automata. Due to the need of guessing for each transition whether it resets the clock, the algorithm is of exponential complexity in the size of the learned automata. Before presenting this algorithm, we propose a simpler version where the teacher is assumed to be smart in the sense of being able to provide the reset information. We show that this simpler setting yields a polynomial complexity of the learning process. Both of the algorithms are implemented and evaluated on a collection of randomly generated examples. We furthermore demonstrate the simpler algorithm on the functional specification of the TCP protocol.