Latticed Craig Interpolation with an Application to Probabilistic Verification

Abstract

In this work, we are primarily concerned with the question: Is Craig interpolation applicable to the automatic, quantitative verification of (infinite-state) probabilistic programs with potentially unbounded loops? Our preliminary results indicate an affirmative answer:

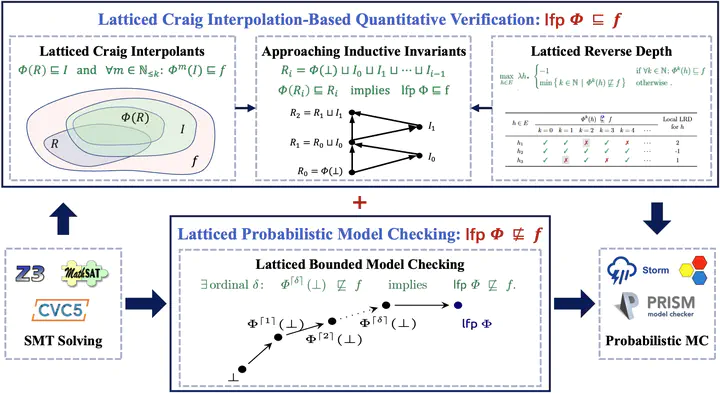
• Quantitative Craig interpolants. We propose a quantitative version of Craig interpolants by extending predicates to expectations (expected values), which can be used to discover quantitative loop invariants that suffice to establish upper bounds on the least fixed point;
• Latticed Craig interpolation. We present latticed Craig interpolation by exploiting quantitative interpolants over complete lattices, which conservatively extends both McMillan’s interpolation-based SAT model checking (to the quantitative setting) and Batz et al.’s latticed bounded model checking (to the unbounded case);
• Soundness and Completeness. We show that our latticed interpolation procedure is sound and establish sufficient conditions under which it is further complete.
• Synthesizing quantitative interpolants. We (semi-)automated our verification procedure by employing a counterexample-guided inductive synthesis framework to automatically generate quantitative interpolants. Our implementation shows promise: It finds invariants for non-trivial infinite-state programs with unbounded loops.