Fixed-Point Reasoning for Stochastic Systems

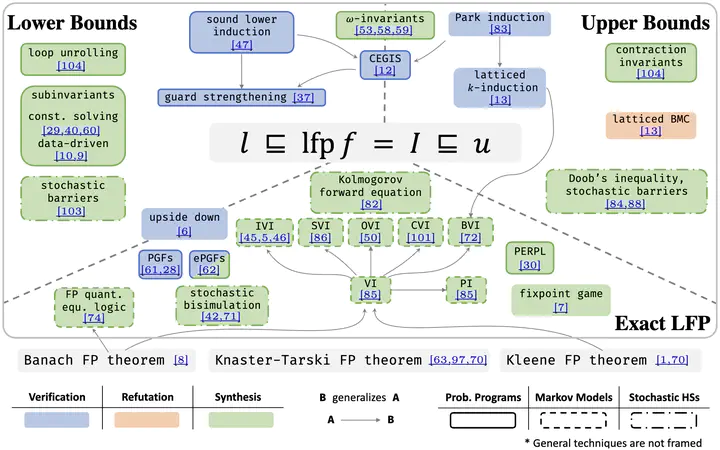
Abstract

Fixed points are mathematical objects that are commonly employed in computer science to characterize key properties of iterative or cyclic behaviors, e.g., unbounded loops and recursions in programs or cycles in transition systems. Reasoning about such behaviors is arguably the hardest task in formal verification. The problem is even harder for stochastic systems as it often amounts to inferring quantitative fixed points that are highly intractable in practice. This article surveys recent advancements in fixed-point reasoning for stochastic systems modeled as probabilistic programs, probabilistic transition systems, and stochastic hybrid systems and outlines potential directions for future research thereof. The core of our results is the fixed-point reasoning landscape for stochastic systems, where we focus on formal techniques that either (i) establish sound over-/under-approximations of quantitative fixed points; or (ii) infer the exact fixed points for a restricted class of systems.